
S. Buswell, O. Caprotti, D. P. Carlisle, M. C. Dewar, M. Gaëtano, M. Kohlhase, J. H. Davenport (revision 1) and P. D.F. Ion (revision 1)

This document describes version 2 revision 1 of OpenMath: a standard for the representation and communication of mathematical objects. This revision clarifies the first OpenMath 2.0 [9]. OpenMath allows the meaning of an object to be encoded rather than just a visual representation. It is designed to allow the free exchange of mathematical objects between software systems and human beings. On the worldwide web it is designed to allow mathematical expressions embedded in web pages to be manipulated and used in computations in a meaningful and correct way. It is designed to be machine-generatable and machine-readable, rather than written by hand.
The OpenMath Standard is the official reference for the OpenMath language and has been approved by the OpenMath Society. It is not intended as an introductory document or a user's guide, for the latest available material of this nature, and the latest version of the standard, please consult the OpenMath web-site at http://www.openmath.org.
This document includes an overview of the OpenMath architecture, an abstract description of OpenMath objects and two mechanisms for producing concrete encodings of such objects. The first, in XML (either innate or Strict Content MathML), is designed primarily for use on the web, in documents, and for applications which want to mix OpenMath as a content representation with MathML as a presentation format. The second, a binary format, is designed for applications which wish to exchange very large objects, or a lot of data as efficiently as possible. This document also includes a description of Content Dictionaries - the mechanism by which the meaning of a symbol in the OpenMath language is encoded, as well as an XML encoding for them. Finally it includes guidelines for the development of OpenMath-compliant applications. Further background on OpenMath and guidelines for its use in applications may be found in the accompanying Primer [10].
This chapter briefly introduces OpenMath concepts and notions that are referred to in the rest of this document.
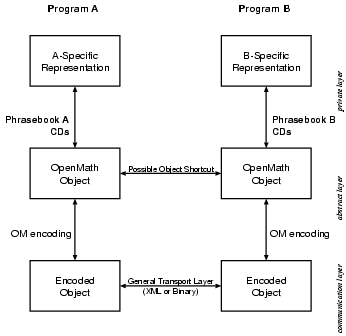
The architecture of OpenMath is described in Figure 1.1 and summarizes the interactions among the different OpenMath components. There are three layers of representation of a mathematical object. The first is a private layer that is the internal representation used by an application. The second is an abstract layer that is the representation as an OpenMath object. Note that these two layers may, in some cases, be the same. The third is a communication layer that translates the OpenMath object representation into a stream of bytes. An application dependent program manipulates the mathematical objects using its internal representation, it can convert them to OpenMath objects and communicate them by using the byte stream representation of OpenMath objects.
This standard does not describe the mechanisms by which software systems may offer, or make use of, computational services. The currently-suggested mechanism is the Symbolic Computation Software Composability Protocol (SCSCP) [1].
OpenMath objects are representations of mathematical entities that can be communicated among various software applications in a meaningful way, that is, preserving their "semantics".
OpenMath objects and encodings are described in detail in Chapter 2 and Chapter 3.
The standard endorses two encodings in XML (an innate one described here, and one in Strict Content MathML) and a binary format. At the time of writing, these are the encodings supported by most existing OpenMath tools and applications, however they are not the only possible encodings of OpenMath objects. Users who wish to define their own encoding, are free to do so provided that there is a well-defined correspondence between the new encoding and the abstract model defined in Chapter 2.
Content Dictionaries (CDs) are used to assign informal and formal semantics to all symbols used in the OpenMath objects. They define the symbols used to represent concepts arising in a particular area of mathematics.
The Content Dictionaries are public, they represent the actual common knowledge among OpenMath applications. Content Dictionaries fix the "meaning" of objects independently of the application. The application receiving the object may then recognize whether or not, according to the semantics of the symbols defined in the Content Dictionaries, the object can be transformed to the corresponding internal representation used by the application.
Several additional files are related to Content Dictionaries. Signature Dictionaries contain the signatures of symbols defined in some OpenMath Content Dictionary and their format is endorsed by this standard.
Furthermore, the standard fixes how to define a specific set of Content Dictionaries as a CDGroup.
Auxiliary files that define presentation and rendering or that are used for manipulating and processing Content Dictionaries are not discussed by the standard.
The conversion of an OpenMath object to/from the internal representation in a software application is performed by an interface program called a Phrasebook. The translation is governed by the Content Dictionaries and the specifics of the application. It is envisioned that a software application dealing with a specific area of mathematics declares which Content Dictionaries it understands. As a consequence, it is expected that the Phrasebook of the application is able to translate OpenMath objects built using symbols from these Content Dictionaries to/from the internal mathematical objects of the application.
OpenMath objects do not specify any computational behaviour, they merely represent mathematical expressions. Part of the OpenMath philosophy is to leave it to the application to decide what it does with an object once it has received it. OpenMath is not a query or programming language. Because of this, OpenMath does not prescribe a way of forcing "evaluation" or "simplification" of objects like or . Thus, the same object could be transformed to by a computer algebra system, or displayed as by a typesetting tool. For such a query/programming language, the OpenMath Society recommends the Symbolic Computation Software Composability Protocol (SCSCP) [1].
In this chapter we provide a self-contained description of OpenMath objects. We first do so by means of an abstract grammar description (Section 2.1) and then give a more informal description (Section 2.2).
OpenMath represents mathematical objects as terms or as labelled trees that are called OpenMath objects or OpenMath expressions. The definition of an abstract OpenMath object is then the following.
The Basic OpenMath Objects form the leaves of the OpenMath Object tree. A Basic OpenMath Object is of one of the following.
(i) Integer.
Integers in the mathematical sense, with no predefined range. They are "infinite precision" integers (also called "bignums" in computer algebra).
(ii) IEEE floating point number.
Double precision floating-point numbers following the IEEE 754-1985 standard [22].
(iii) Character string.
A Unicode Character string. This also corresponds to "characters" in XML.
(iv) Bytearray.
A sequence of bytes.
(v) Symbol.
A Symbol encodes three fields of information, a symbol name, a Content Dictionary name, and (optionally) a Content Dictionary base URI, The name of a symbol is a sequence of characters matching the regular expression described in Section 2.3. The Content Dictionary is the location of the definition of the symbol, consisting of a name (a sequence of characters matching the regular expression described in Section 2.3) and, optionally, a unique prefix called a cdbase which is used to disambiguate multiple Content Dictionaries of the same name. There are other properties of the symbol that are not explicit in these fields but whose values may be obtained by inspecting the Content Dictionary specified. These include the symbol definition, formal properties and examples and, optionally, a Role which is a restriction on where the symbol may appear in an OpenMath object. The possible roles are described in Section 2.1.4.
(vi) Variable.
A Variable must have a name which is a sequence of characters matching a regular expression, as described in Section 2.3.
Derived OpenMath objects are currently used as a way by which non-OpenMath data is embedded inside an OpenMath object. A derived OpenMath object is built as follows:
(i) If is not an OpenMath object, then is an OpenMath foreign object. An OpenMath foreign object may optionally have an encoding field which describes how its contents should be interpreted.
OpenMath objects are built recursively as follows.
(i) Basic OpenMath objects are OpenMath objects. (Note that derived OpenMath objects are not OpenMath objects, but are used to construct OpenMath objects as described below.)
(ii) If , …, are OpenMath objects, then is an OpenMath application object.
(iii) If are OpenMath symbols, and is an OpenMath object, and , …, are OpenMath objects or OpenMath derived objects, then is an OpenMath attribution object.
is the object stripped of attributions. are referred to as keys and , …, as their associated values. If, after recursively applying stripping to remove attributions, the resulting un-attributed object is a variable, the original attributed object is called an attributed variable.
(iv) If and are OpenMath objects, and , , are OpenMath variables or attributed variables, then is an OpenMath binding object.
(v) If is an OpenMath symbol and , …, are OpenMath objects or OpenMath derived objects, then is an OpenMath error object.
OpenMath objects that are contstructed via rules (ii) to (v) are jointly called compound OpenMath objects
We say that an OpenMath symbol is used to construct an OpenMath object if it is the first child of an OpenMath application, binding or error object, or an even-indexed child of an OpenMath attribution object (i.e. the key in a (key, value) pair). The role of an OpenMath symbol is a restriction on how it may be used to construct a compound OpenMath object and, in the case of the key in an attribution object, a clarification of how that attribution should be interpreted. The possible roles are:
binder The symbol may appear as the first child of an OpenMath binding object.
attribution The symbol may be used as key in an OpenMath attribution object, i.e. as the first element of a (key, value) pair, or in an equivalent context (for example to refer to the value of an attribution). This form of attribution may be ignored by an application, so should be used for information which does not change the meaning of the attributed OpenMath object.
semantic-attribution This is the same as attribution except that it modifies the meaning of the attributed OpenMath object and thus cannot be ignored by an application, without changing the meaning.
error The symbol may appear as the first child of an OpenMath error object.
application The symbol may appear as the first child of an OpenMath application object.
constant The symbol cannot be used to construct an OpenMath compound object.
A symbol cannot have more than one role and cannot be used to construct a compound OpenMath object in a way which requires a different role (using the definition of construct given earlier in this section). This means that one cannot use a symbol which binds some variables to construct, say, an application object. However it does not prevent the use of that symbol as an argument in an application object (where by argument we mean a child with index greater than 1).
If no role is indicated then the symbol can be used anywhere. Note that this is not the same as saying that the symbol's role is constant.
Informally, an OpenMath object can be viewed as a tree and is also referred to as a term. The objects at the leaves of OpenMath trees are called basic objects. The basic objects supported by OpenMath are:
Arbitrary Precision integers.
OpenMath floats are IEEE 754 Double precision floating-point numbers. Other types of floating point number may be encoded in OpenMath by the use of suitable content dictionaries.
are sequences of characters. These characters come from the Unicode standard [12].
are sequences of bytes. There is no "byte" in OpenMath as an object of its own. However, a single byte can of course be represented by a bytearray of length 1. The difference between strings and bytearrays is the following: a character string is a sequence of bytes with a fixed interpretation (as characters, Unicode texts may require several bytes to code one character), whereas a bytearray is an uninterpreted sequence of bytes with no intrinsic meaning. Bytearrays could be used inside OpenMath errors to provide information to, for example, a debugger; they could also contain intermediate results of calculations, or "handles" into computations or databases.
are uniquely defined by the Content Dictionary in which they occur
and by a name.
The form of these definitions is explained in
Chapter 4. Each symbol has no more than one
definition in a Content Dictionary. Many Content Dictionaries may
define differently a symbol with the same name (e.g. the symbol
union is defined as
associative-commutative set theoretic union in a Content Dictionary
set1 but another Content Dictionary,
multiset1 might define a symbol
union as the union of multi-sets).
are meant to denote parameters, variables or indeterminates (such as bound variables of function definitions, variables in summations and integrals, independent variables of derivatives).
Derived OpenMath objects are constructed from non-OpenMath data. They differ from bytearrays in that they can have any structure. Currently there is only one way of making a derived OpenMath object.
is used to import a non-OpenMath object into an OpenMath attribution. Examples of its use could be to annotate a formula with a visual or aural rendering, an animation, etc. They may also appear in OpenMath error objects, for example to allow an application to report an error in processing such an object.
The four following constructs can be used to make compound OpenMath objects out of basic or derived OpenMath objects.
constructs an OpenMath object from a sequence of one or more OpenMath objects. The first child of an application is referred to as its "head" while the remaining objects are called its "arguments". An OpenMath application object can be used to convey the mathematical notion of application of a function to a set of arguments. For instance, suppose that the OpenMath symbol is defined in a suitable Content Dictionary, then is the abstract OpenMath object corresponding to . More generally, an OpenMath application object can be used as a constructor to convey a mathematical object built from other objects such as a polynomial constructed from a set of monomials. Constructors build inhabitants of some symbolic type, for instance the type of rational numbers or the type of polynomials. The rational number, usually denoted as , is represented by the OpenMath application object . The symbol must be defined, by a Content Dictionary, as a constructor symbol for the rational numbers.
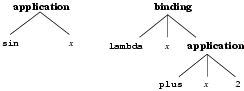
objects are constructed from an OpenMath object, and from a sequence of zero or more variables followed by another OpenMath object. The first OpenMath object is the "binder" object. Arguments 2 to are always variables to be bound in the "body" which is the (last) argument object. It is allowed to have no bound variables, but the binder object and the body should be present. Binding can be used to express functions or logical statements. The function , in which the variable is bound by , corresponds to a binding object having as binder the OpenMath symbol :
Phrasebooks are allowed to use conversion in order to avoid clashes of variable names. Suppose an object contains an occurrence of the object . This object can be replaced in by where is a variable not occurring free in and is obtained from by replacing each free (i.e., not bound by any intermediate binding construct) occurrence of by . This operation preserves the semantics of the object . In the above example, a phrasebook is thus allowed to transform the object to, e.g.
Repeated occurrences of the same variable in a binding operator are allowed. An OpenMath application should treat a binding with multiple occurrences of the same variable as equivalent to the binding in which all but the last occurrence of each variable is replaced by a new variable which does not occur free in the body of the binding. is semantically equivalent to: so that the resulting function is actually a constant in its first argument ( does not occur free in the body ).
decorates an object with a sequence of one or more pairs made up of an OpenMath symbol, the "attribute", and an associated object, the "value of the attribute". The value of the attribute can be an OpenMath attribution object itself. As an example of this, consider the OpenMath objects representing groups, automorphism groups, and group dimensions. It is then possible to attribute an OpenMath object representing a group by its automorphism group, itself attributed by its dimension.
OpenMath objects can be attributed with OpenMath foreign objects, which are containers for non-OpenMath structures. For example a mathematical expression could be attributed with its spoken or visual rendering.
Composition of attributions, as in is semantically equivalent to a single attribution, that is The operation that produces an object with a single layer of attribution is called flattening.
Multiple attributes with the same name are allowed. While the order of the given attributes does not imply any notion of priority, potentially it could be significant. For instance, consider the case in which ( ) in the example above. Then, the object is to be interpreted as if the value overwrites the value . (OpenMath however does not mandate that an application preserves the attributes or their order.)
Attribution acts as either adornment annotation or as semantical annotation. When the key has role attribution, then replacement of the attributed object by the object itself is not harmful and preserves the semantics. When the key has role semantic-attribution then the attributed object is modified by the attribution and cannot be viewed as semantically equivalent to the stripped object. If the attribute lacks the role specification then attribution is acting as adornment annotation.
Objects can be decorated in a multitude of ways. An example of the use of an adornment attribution would be to indicate the colour in which an OpenMath object should be displayed, for example . Note that both and are arbitary OpenMath objects whereas is a symbol. An example of the use of a semantic attribution would be to indicate the type of an object. For example the object represents the judgment stating that object has type . Note that both and are arbitary OpenMath objects whereas is a symbol.
is made up of an OpenMath symbol and a sequence of zero or more OpenMath objects. This object has no direct mathematical meaning. Errors occur as the result of some treatment on an OpenMath object and are thus of real interest only when some sort of communication is taking place. Errors may occur inside other objects and also inside other errors. Error objects might consist only of a symbol as in the object: .
The names of symbols, variables and content dictionaries must
conform to the production Name specified in the following
grammar
(which is identical to that for XML names in XML 1.1,
[17]). Informally speaking, a name is a sequence
of Unicode [12]
characters which begins with a letter and cannot contain
certain punctuation and combining characters. The notation
#x... represents the hexadecimal value of
the encoding of a Unicode character.
Some of the character values or code points in the
following productions are currently unassigned, but this is
likely to change in the future as Unicode evolves*1.
*1 We note that in XML 1 the name production explicitly listed the characters that were allowed, so all the characters added in versions of Unicode after 2.0 (which amounted to tens of thousands of characters) were not allowed in names.
Name NameStartChar (NameChar)* NameStartChar ":" | [A-Z] | "_" | [a-z] | [#xC0-#xD6] | [#xD8-#xF6] | [#xF8-#x2FF] | [#x370-#x37D] | [#x37F-#x1FFF] | [#x200C-#x200D] | [#x2070-#x218F] | [#x2C00-#x2FEF] | [#x3001-#xD7FF] | [#xF900-#xFDCF] | [#xFDF0-#xFFFD] | [#x10000-#xEFFFF] NameChar NameStartChar | "-" | "." | [0-9] | #xB7 | [#x0300-#x036F] | [#x203F-#x2040]
CD Base A cdbase must conform to the grammar for URIs described in [7]. Note that if non-ASCII characters are used in a CD or symbol name then when a URI for that symbol is constructed it will be necessary to map the non-ASCII characters to a sequence of octets. The precise mechanism for doing this depends on the URI scheme.
Note on content dictionary names It is a common convention to store a Content Dictionary in a file of the same name, which can cause difficulties on many file systems. If this convention is to be followed then OpenMath recommends that the name be restricted to the subset of the above grammar which is a legal POSIX [6] filename, namely:
Name (PosixLetter | '_') (Char)* Char PosixLetter | Digit | '.' | '-' | '_' PosixLetter 'a' | 'b' | ... | 'z' | 'A' | 'B' | ... | 'Z' Digit '0' | '1' | ... | '9'
Canonical URIs for Symbols To facilitate the use of OpenMath within a URI-based framework (such as RDF [21] or OWL [20]), we provide the following scheme for constructing a canonical URI for an OpenMath Symbol:
URI = cdbase-value + '/' + cd-value + '#' + name-value
So for example the URI for the symbol with cdbase
http://www.openmath.org/cd, cd
transc1 and name sin
is:
http://www.openmath.org/cd/transc1#sin
In particular, this now allows us to refer uniquely to an OpenMath symbol from a MathML-2 document [18] (see [19] section 4.2.3 for MathML-3):
<mathml:csymbol xmlns:mathml="http://www.w3.org/1998/Math/MathML/"
definitionURL="http://www.openmath.org/cd/transc1#sin">
<mo> sin </mo>
</mathml:csymbol>
OpenMath supports basic objects like integers, symbols, floating-point numbers, character strings, bytearrays, and variables.
OpenMath compound objects are of four kinds: applications, bindings, errors, and attributions.
OpenMath objects may be attributed with non-OpenMath objects via the use of foreign OpenMath objects.
OpenMath objects have the expressive power to cover all areas of computational mathematics.
Observe that an OpenMath application object is viewed as a "tree" by software applications that do not understand Content Dictionaries, whereas a Phrasebook that understands the semantics of the symbols, as defined in the Content Dictionaries, should interpret the object as functional application, constructor, or binding accordingly. Thus, for example, for some applications, the OpenMath object corresponding to may result in a command that writes .
In this chapter, two encodings are defined that map between OpenMath objects and byte streams. These byte streams constitute a low level representation that can be easily exchanged between processes (via almost any communication method) or stored and retrieved from files. In addition, OpenMath can be represented in Strict Content MathML, as described in Section 4.1.3 of [19].
The first encoding is the innate character-based encoding in XML format. In previous versions of the OpenMath Standard this encoding was a restricted subset of the full legal XML syntax. In this version, however, we have removed all these restrictions so that the earlier encoding is a strict subset of the existing one. The XML encoding can be used, for example, to send OpenMath objects via e-mail, cut-and-paste, etc. and to embed OpenMath objects in XML documents or to have OpenMath objects processed by XML-aware applications.
The second encoding is a binary encoding that is meant to be used when the compactness of the encoding is important (inter-process communications over a network is an example).
Note that these two encodings are sufficiently different for auto-detection to be effective: an application reading the bytes can very easily determine which encoding is used. In the case of the MathML encoding, the reading application should already be expecting MathML.
This encoding has been designed with two main goals in mind:
to provide an encoding that uses common character sets (so that it can easily be included in most documents and transport protocols) and that is both readable and writable by a human.
to provide an encoding that can be included (embedded) in XML documents or processed by XML-aware applications.
The XML encoding of an OpenMath object is defined by the Relax NG schema [8] given below. Relax NG has a number of advantages over the older XSD Schema format [13], in particular it allows for tighter control of attributes and has a modular, extensible structure. Although we have made the XML form, which is given in Appendix B, normative, it is generated from the compact syntax given below. It is also very easy to restrict the schema to allow a limited set of OpenMath symbols as described in Appendix C.
Standard tools exist for generating a DTD or an XSD schema from a Relax NG Schema. Examples of such documents are given in Appendix E and Appendix D, respectively.
# RELAX NG Schema for OpenMath 2 default namespace om = "http://www.openmath.org/OpenMath" start = OMOBJ # OpenMath object constructor OMOBJ = element OMOBJ { compound.attributes, attribute version { xsd:string }?, omel } # Elements which can appear inside an OpenMath object omel = OMS | OMV | OMI | OMB | OMSTR | OMF | OMA | OMBIND | OME | OMATTR |OMR # things which can be variables omvar = OMV | attvar attvar = element OMATTR { common.attributes,(OMATP , (OMV | attvar))} cdbase = attribute cdbase { xsd:anyURI}? # attributes common to all elements common.attributes = (attribute id { xsd:ID })? # attributes common to all elements that construct compount OM objects. compound.attributes = common.attributes,cdbase # symbol OMS = element OMS { common.attributes, attribute name { xsd:NCName}, attribute cd { xsd:NCName}, cdbase } # variable OMV = element OMV { common.attributes, attribute name { xsd:NCName} } # integer OMI = element OMI { common.attributes, xsd:string {pattern = "\s*(-\s?)?[0-9]+(\s[0-9]+)*\s*"}} # byte array OMB = element OMB { common.attributes, xsd:base64Binary } # string OMSTR = element OMSTR { common.attributes, text } # IEEE floating point number OMF = element OMF { common.attributes, ( attribute dec { xsd:double } | attribute hex { xsd:string {pattern = "[0-9A-F]+"}}) } # apply constructor OMA = element OMA { compound.attributes, omel+ } # binding constructor OMBIND = element OMBIND { compound.attributes, omel, OMBVAR, omel } # variables used in binding constructor OMBVAR = element OMBVAR { common.attributes, omvar+ } # error constructor OME = element OME { common.attributes, OMS, (omel|OMFOREIGN)* } # attribution constructor and attribute pair constructor OMATTR = element OMATTR { compound.attributes, OMATP, omel } OMATP = element OMATP { compound.attributes, (OMS, (omel | OMFOREIGN) )+ } # foreign constructor OMFOREIGN = element OMFOREIGN { compound.attributes, attribute encoding {xsd:string}?, (omel|notom)* } # Any elements not in the om namespace # (valid om is allowed as a descendant) notom = (element * - om:* {attribute * { text }*,(omel|notom)*} | text) # reference constructor OMR = element OMR { common.attributes, attribute href { xsd:anyURI } }
Note:
In the original edition of OpenMath 2.0 as published, names are specified
as being of the xsd:NCName type.
When the original edition of OpenMath 2.0 was published,
W3C Schema types were defined in terms of XML 1 [15].
This limited the characters allowed in a name to a
subset of the characters available in Unicode 2.0, which was far more
restrictive than the definition for an OpenMath name given in Section 2.3.
The situation has changed with the appearance of XML 1.0 5th edition,
and more specifically erratum NE17 in [16],
and there is no known contradiction remaining.
An encoded OpenMath object is placed inside an OMOBJ element. This
element can contain the elements (and integers) described above.
It can take an optional
version (XML) attribute which indicates to
which version of the OpenMath standard it conforms. In previous versions of
this standard this attribute did not exist, so any OpenMath object without
such an attribute must conform to version 1 (or equivalently 1.1) of the
OpenMath standard. Objects which conform to the description given in this
document should have version="2.0".
We briefly discuss the XML encoding for each type of OpenMath object starting from the basic objects.
are encoded using the
OMI element around the sequence of their
digits in base 10 or 16 (most significant digit first). White space
may be inserted between the characters of the integer representation,
this will be ignored. After ignoring white space, integers written in
base 10 match the regular expression
-?[0-9]+. Integers written in base 16 match
-?x[0-9A-F]+. The integer 10 can be thus
encoded as <OMI> 10 </OMI> or as
<OMI> xA </OMI> but neither
<OMI> +10 </OMI> nor
<OMI> +xA </OMI> can be used.
The negative integer
can be encoded
as either as decimal <OMI> -120
</OMI> or as hexadecimal <OMI>
-x78 </OMI>.
are encoded using
the OMS element. This element has
three
(XML) attributes cd,
name, and
cdbase. The value of
cd is the name of the Content Dictionary in
which the symbol is defined and the value of
name is the name of the symbol.
The optional cdbase
attribute is a URI that can be used to disambiguate between two content
dictionaries with the same name.
If a symbol does not have an explicit cdbase
attribute, then it inherits its cdbase from the
first ancestor in the XML tree with one, should such an element
exist. In this document we have tended to omit the
cdbase for clarity.
For example:
<OMS cdbase="http://www.openmath.org/cd" cd="transc1" name="sin"/>
is the encoding of the symbol named sin in
the Content Dictionary named transc1,
which is part of the collection
maintained by the OpenMath Society.
As described in Section 2.3,
the three attributes of the
OMS can be used to build a URI reference for the symbol,
for use in contexts where URI-based referencing mechanisms are used.
For example the URI for the above symbol is
http://www.openmath.org/cd/transc1#sin.
Note that the role attribute described in Section 2.1.4 is contained in the Content Dictionary and is not
part of the encoding of a symbol, also the cdbase attribute need not
be explicit on each OMS as it is inherited
from any ancestor element.
are encoded using
the OMV element, with only one
(XML) attribute, name, whose value is the
variable name. For instance, the encoding of the object
representing the variable
is:
<OMV name="x"/>
are
encoded using the OMF element that has
either the (XML) attribute dec or the
(XML) attribute hex. The two
(XML) attributes cannot be present simultaneously. The value of
dec is the floating-point number expressed
in base 10, using the common syntax:
(-?)([0-9]+)?("."[0-9]+)?([eE](-?)[0-9]+)?.or one of the special values: INF, -INF or NaN.
The value of
hex is a base 16 representation of the
64 bits of the IEEE Double.
Thus the number represents mantissa, exponent, and sign in network byte order.
This consists of a string of 16 digits 0-9, A-F.
For example, both <OMF
dec="1.0e-10"/> and
<OMF hex="3DDB7CDFD9D7BDBB"/>
are valid representations of the floating point number
.
The symbols INF,
-INF and NaN represent
positive and negative infinity, and not a number as
defined in [22]. Note that while infinities
have a unique representation, it is possible for NaNs to contain extra
information about how they were generated and if this informations is to
be preserved then the hexadecimal representation must be used. For
example
<OMF hex="FFF8000000000000"/> and
<OMF hex="FFF8000000000001"/> are both
hexadecimal representations of NaNs.
are encoded using the OMSTR element.
Its content is a Unicode text. Note that as always in XML the
characters < and & need to be represented by the
entity references < and
& respectively.
are encoded using the OMB element. Its content
is a sequence of characters that is a base64 encoding of the data.
The base64 encoding is defined in RFC
2045 [2].
Basically, it represents an arbitrary sequence of octets using 64
"digits" (A through Z, a through z, 0 through 9, + and /, in order of increasing
value). Three octets are represented as four digits (the =
character is used for padding at the end of the data). All line
breaks and carriage return, space, form feed and horizontal
tabulation characters are ignored. The reader is referred to
[2]
for more detailed information.
are encoded using the OMA element. The
application whose head is the OpenMath object
and whose arguments
are the OpenMath objects
, …,
is encoded as <OMA>
…
</OMA> where
is the encoding of
.
For example, is encoded as:
<OMA> <OMS cd="transc1" name="sin"/> <OMV name="x"/> </OMA>
provided that the symbol sin is defined to be a function
symbol in a Content Dictionary named transc1.
is encoded using the OMBIND element. The binding
by the OpenMath object
of the OpenMath variables
,
,
,
in the object
is encoded as <OMBIND>
<OMBVAR>
</OMBVAR>
</OMBIND> where
,
, and
are the encodings of
,
and
, respectively.
For instance the encoding of is:
<OMBIND>
<OMS cd="fns1" name="lambda"/>
<OMBVAR><OMV name="x"/></OMBVAR>
<OMA>
<OMS cd="transc1" name="sin"/>
<OMV name="x"/>
</OMA>
</OMBIND>Binders are defined in Content Dictionaries, in particular,
the symbol lambda is defined in the Content Dictionary
fns1 for functions over functions.
are encoded using the OMATTR element. If
the OpenMath object
is attributed with (
,
), …,
(
,
) pairs (where
are the attributes), it is encoded
as <OMATTR> <OMATP>
…
</OMATP>
</OMATTR> where
is the encoding of the
symbol
,
of the object
and
is the encoding of
.
Examples are the use of attribution to decorate a group by its automorphism group:
<OMATTR>
<OMATP>
<OMS cd="groups" name="automorphism_group" />
[..group-encoding..]
</OMATP>
[..group-encoding..]
</OMATTR>or to express the type of a variable:
<OMATTR>
<OMATP>
<OMS cd="ecc" name="type" />
<OMS cd="ecc" name="real" />
</OMATP>
<OMV name="x" />
</OMATTR>
A special use of attributions is to associate non-OpenMath data with an
OpenMath object. This is done using the
OMFOREIGN element. The children of this
element must be well-formed XML. For example the attribution of the
OpenMath object
with its
representation in Presentation MathML is:
<OMATTR>
<OMATP>
<OMS cd="annotations1" name="presentation-form"/>
<OMFOREIGN encoding="MathML-Presentation">
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mi>sin</mi><mfenced><mi>x</mi></mfenced>
</math>
</OMFOREIGN>
</OMATP>
<OMA>
<OMS cd="transc1" name="sin"/>
<OMV name="x"/>
</OMA>
</OMATTR>
Of course not everything has a natural XML encoding in this way and
often the contents of a OMFOREIGN will just
be data or some kind of encoded string. For example the attribution
of the previous object with its LaTeX representation could be achieved
as follows:
<OMATTR>
<OMATP>
<OMS cd="annotations1" name="presentation-form"/>
<OMFOREIGN encoding="text/x-latex">\sin(x)</OMFOREIGN>
</OMATP>
<OMA>
<OMS cd="transc1" name="sin"/>
<OMV name="x"/>
</OMA>
</OMATTR>
For a discussion on the use of the encoding
attribute see Section 5.2.
are encoded using the OME element. The error whose
symbol is
and whose arguments are the OpenMath objects
or OpenMath derived objects
,
…,
is encoded as <OME>
…
</OME> where
is the encoding of
and
the encoding
of
.
If an aritherror Content Dictionary contained a
DivisionByZero symbol, then the object
would be encoded as follows:
<OME>
<OMS cd="aritherror" name="DivisionByZero"/>
<OMA>
<OMS cd="arith1" name="divide" />
<OMV name="x"/>
<OMI> 0 </OMI>
</OMA>
</OME>
If a mathml Content Dictionary contained an
unhandled_csymbol symbol, then an OpenMath to
MathML translator might return an error such as:
<OME>
<OMS cd="mathml" name="unhandled_csymbol"/>
<OMFOREIGN encoding="MathML-Content">
<mathml:csymbol xmlns:mathml="http://www.w3.org/1998/Math/MathML/"
definitionURL="http://www.nag.co.uk/Airy#A">
<mathml:mo>Ai</mathml:mo>
</mathml:csymbol>
</OMFOREIGN>
</OME> Note that it is possible to embed fragments
of valid OpenMath inside an OMFOREIGN element but that it
cannot contain invalid OpenMath. In addition, the arguments to an
OMERROR must be well-formed XML. If an
application wishes to signal that the OpenMath it has received is invalid or
is not well-formed then the offending data must be encoded as a string.
For example:
<OME>
<OMS cd="parser" name="invalid_XML"/>
<OMSTR>
<OMA> <OMS name="cos" cd="transc1">
<OMV name="v"> </OMA>
</OMSTR>
</OME>Note that the "<" and ">" characters have been escaped as is usual in an XML document.
OpenMath integers, floating point numbers, character strings,
bytearrays, applications, binding, attributions can also be encoded
as an empty OMR element with an href
attribute whose value is the value of a URI referencing an id
attribute of an OpenMath object of that type.
The OpenMath element represented by this OMR
reference is a copy of the OpenMath element referenced
href attribute. Note that this copy
is structurally equal, but not identical
to the element referenced. These URI
refererences will often be relative, in which case they are resolved using
the base URI of the document containing the OpenMath.
For instance, the OpenMath object
can be encoded in the XML encoding as either one of the XML encodings given in Figure 3.1 (and some intermediate versions as well).
We say that an OpenMath element dominates all its children and all elements
they dominate. An OMR element dominates its target,
i.e. the element that carries the id attribute pointed to
by the xref attribute. For instance in the representation
in Figure 3.1, the
OMA element with id="t1" and
also the second OMR dominate the
OMA element with id="t11".
The occurrences of the OMR element must obey the following global
acyclicity constraint: An OpenMath element may not dominate itself.
Consider for instance the following (illegal) XML representation
<OMOBJ version="2.0">
<OMA id="foo">
<OMS cd="arith1" name="divide"/>
<OMI>1</OMI>
<OMA>
<OMS cd="arith1" name="plus"/>
<OMI>1</OMI>
<OMR xref="foo"/>
</OMA>
</OMA>
</OMOBJ>
Here, the OMA element with
id="foo" dominates its third child, which dominates the
OMR element, which dominates its target: the element with
id="foo". So by transitivity, this element dominates itself, and
by the acyclicity constraint, it is not the XML representation of an OpenMath
element. Even though it could be given the interpretation of the continued fraction
this would correspond to an infinite tree of applications,
which is not admitted by the structure of OpenMath objects described
in Chapter 2.
Note that the acyclicity constraints is not restricted to such simple cases, as the example in Figure 3.2 shows.
<OMOBJ version="2.0"> <OMOBJ version="2.0">
<OMA id="bar"> <OMA id="baz">
<OMS cd="arith1" name="plus"/> <OMS cd="arith1" name="plus"/>
<OMI>1</OMI> <OMI>1</OMI>
<OMR xref="baz"/> <OMR xref="bar"/>
</OMA> </OMA>
</OMOBJ> </OMOBJ>
Here, the OMA with
id="bar" dominates its third child, the
OMR with xref="baz",
which dominates its target OMA with
id="baz", which in turn dominates its third
child, the OMR with
xref="bar", this finally dominates its
target, the original OMA element with
id="bar". So this pair of OpenMath objects
violates the acyclicity constraint and is not the XML
representation of an OpenMath object.
Note that the OMR element is a
syntactic referencing mechanism: an
OMR element stands for the exact XML
element it points to. In particular, referencing does not interact
with binding in a semantically intuitive way, since it allows for
variable capture. Consider for instance the following XML
representation:
<OMBIND id="outer">
<OMS cd="fns1" name="lambda"/>
<OMBVAR><OMV name="X"/></OMBVAR>
<OMA>
<OMV name="f"/>
<OMBIND id="inner">
<OMS cd="fns1" name="lambda"/>
<OMBVAR><OMV name="X"/></OMBVAR>
<OMR id="copy" href="#orig"/>
</OMBIND>
<OMA id="orig"><OMV name="g"/><OMV name="X"/></OMA>
</OMA>
</OMBIND>
it represents the OpenMath object
which has two sub-terms of the form
, one with id="orig" (the one explicitly
represented) and one with id="copy", represented by the
OMR element. In the original, the variable
is bound by the outer
OMBIND element, and in the copy, the variable
is bound by the inner
OMBIND element. We say that the inner
OMBIND has captured the variable
.
It is well-known that variable capture does not conserve semantics. For instance, we could use -conversion to rename the inner occurrence of into, say, arriving at the (same) object Using references that capture variables in this way can easily lead to representation errors, and is not recommended.
The above encoding of XML encoded OpenMath specifies the grammar to be used in files that encode a single OpenMath object, and specifies the character streams that a conforming OpenMath application should be able to accept or produce.
When embedding XML encoded OpenMath objects into a larger XML document
one may wish, or need, to use other XML features. For example use of
extra XML attributes to specify XML Namespaces [14]
or xml:lang attributes to specify the language used in
strings [17].
If such XML features are used then the XML application controlling the document must, if passing the OpenMath fragment to an OpenMath application, remove any such extra attributes and must ensure that the fragment is encoded according to the schema specified above.
The binary encoding was essentially designed to be more compact than the XML encodings, so that it can be more efficient if large amounts of data are involved. For the current encoding, we tried to keep the right balance between compactness, speed of encoding and decoding and simplicity (to allow a simple specification and easy implementations).
| start | [24] object [25] | | | [24+64] [ ] [ ] object [25] | |
| object | basic | |||
| | | compound | |||
| | | cdbase | |||
| | | foreign | |||
| | | reference | |||
| basic | integer | |||
| | | float | |||
| | | variable | |||
| | | symbol | |||
| | | string | |||
| | | bytearray | |||
| integer | [1] [_] | | | [1+64] [ ] id: [_] | |
| [1+32] [_] | ||||
| | | [1+128] {_} | | | [1+64+128] { } id: {_} | |
| | | [1+32+128] {_} | |||
| | | [2] [ ] [_] digits: | | | [2+64] [ ] [ ] [_] digits: id: | |
| | | [2+32] [ ] [_] digits: | |||
| | | [2+128] { } [_] digits: | | | [2+64+128] { } { } [_] digits: id: | |
| | | [2+32+128] { } [_] digits: | |||
| float | [3] {_}{_} | | | [3+64] [ ] id: {_}{_} | |
| | | [3+64+128] { } id: {_}{_} | |||
| variable | [5] [ ] varname: | | | [5+64] [ ] [ ] varname: id: | |
| | | [5+128] { } varname: | | | [5+64+128] { } { } varname: id: | |
| symbol | [8] [ ] [ ] cdname: symbname: | | | [8+64] [ ] [ ] [ ] cdname: symbname: id: | |
| | | [8+128] { } { } cdname: symbname: | | | [8+64+128] { } { } { } cdname: symbname: id: | |
| string | [6] [ ] bytes: | | | [6+64] [ ] bytes: | |
| [6+32] [ ] bytes: | ||||
| | | [6+128] { } bytes: | | | [6+64+128] { } { } bytes: id: | |
| | | [6+32+128] { } bytes: | |||
| | | [7] [ ] bytes: | | | [7+64] [ ] [ ] bytes: id: | |
| | | [7+32] [ ] bytes: | |||
| | | [7+128] { } bytes: | | | [7+64+128] { } { } bytes: id: | |
| | | [7+32+128] { } bytes: | |||
| bytearray | [4] [ ] bytes: | | | [4+64] [ ] [ ] bytes: id: | |
| [4+32] [ ] bytes: | ||||
| | | [4+128] { } bytes: | | | [4+64+128] { } { } bytes: id: | |
| | | [4+32+128] { } bytes: | |||
| cdbase | [9] [ ] uri: object | |||
| | | [9+128] { } uri: object | |||
| foreign | [12] [ ] [ ] bytes: bytes: | | | [12+64] [ ] [ ] [ ] bytes: bytes: id: | |
| [12+32] [ ] [ ] bytes: bytes: | ||||
| | | [12+128] { } { } bytes: bytes: | | | [12+64+128] { } { } { } bytes: bytes: id: | |
| | | [12+32+128] { } { } bytes: bytes: | |||
| compound | application | |||
| | | binding | |||
| | | attribution | |||
| | | error | |||
| application | [16] object objects [17] | | | [16+64] [ ] id: object objects [17] | |
| | | [16+64+128] { } id: object objects [17] | |||
| binding | [26] object bvars object [27] | | | [26+64] [ ] id: object bvars object [27] | |
| | | [26+64+128] { } id: object bvars object [27] | |||
| attribution | [18] attrpairs object [19] | | | [18+64] [ ] id: attrpairs object [19] | |
| | | [18+64+128] { } id: attrpairs object [19] | |||
| error | [22] symbol objects [23] | | | [22+64] [ ] id: symbol objects [23] | |
| | | [22+64+128] { } id: symbol objects [23] | |||
| attrpairs | [20] pairs [21] | | | [20+64] [ ] id: pairs [21] | |
| | | [20+64+128] { } id: pairs [21] | |||
| pairs | symbol object | |||
| | | symbol object pairs | |||
| bvars | [28] vars [29] | | | [28+64] [ ] id: vars [29] | |
| | | [28+64+128] { } id: vars [29] | |||
| vars | empty | |||
| | | attrvar vars | |||
| attrvar | variable | |||
| | | [18] attrpairs attrvar [19] | | | [18+64] [ ] id: attrpairs attrvar [19] | |
| | | [18+64+128] { } id: attrpairs attrvar [19] | |||
| objects | empty | |||
| | | object objects | |||
| reference | internal_reference | |||
| | | external_reference | |||
| internal_reference | [30] [_] | |||
| | | [30+128] {_} | |||
| external_reference | [31] [ ] uri: | |||
| | | [31+128] { } uri: |
Figure 3.3 gives a grammar for the binary encoding ("start" is the start symbol)..
The following conventions are used in this section: [ ] denotes a byte whose value is the integer ( can range from 0 to 255), { } denotes four bytes representing the (unsigned) integer in network byte order, [_] denotes an arbitrary byte, {_} denotes an arbitrary sequence of four bytes. Finally, empty stands for the empty list of tokens.
xxxx: , where xxxx is one of symbname, cdname, varname, uri, id, digits, or bytes denotes a sequence of bytes that conforms to the constraints on xxxx strings. For instance, for symbname, varname, or cdname this is the regular expression described in Section 2.3, for uri it is the grammar for URIs in [7].
An OpenMath object is encoded as a sequence of bytes starting with the begin object tag
(values 24 and 88) and ending with the end
object tag (value 25). These are similar to
the <OMOBJ> and </OMOBJ> tags of
the XML encoding. Objects with start token [88]
have two additional bytes
and
that characterize the version
(
) of the encoding
directly after the start token. This is similar to <OMOBJ
version="m.n">
The encoding of each kind of OpenMath object begins with a tag that is a single byte, holding a token identifier that describes the kind of object, two flags, and a status bit. The identifier is stored in the first five bits (1 to 5). Bit 6 is used as a status bit which is currently only used for managing streaming of some basic objects. Bits 7 and 8 are the sharing flag and the long flag. The sharing flag indicates that the encoded object may be shared in another (part of an) object somewhere else (see Section 3.2.4.2). Note that if the sharing flag is set (in the right column of the grammar in Figure 3.3, then the encoding includes a representation of an identifier that serves as the target of a reference (internal with token identifier 30 or external with token identifier 31). If the long flag is set, this signifies that the names, strings, and data fields in the encoded OpenMath object are longer than 255 bytes or characters.
The concept of structure sharing in OpenMath encodings and in particular the sharing bit in the binary encoding has been introduced in OpenMath 2 (see section Section 3.2.4.2 for details). The binary encoding in OpenMath 2 leaves the tokens with sharing flag 0 unchanged to ensure OpenMath 1 compatibility. To make use of functionality like the version attribute on the OpenMath object introduced in OpenMath 2, the tokens with sharing flag 1 should be used.
To facilitate the streaming of OpenMath objects, some basic objects (integers, strings, bytearrays, and foreign objects) have variant token identifiers with the fifth bit set. The idea behind this is that these basic objects can be split into packets. If the fifth bit is not set, this packet is the final packet of the basic object. If the bit is set, then more packets of the basic object will follow directly after this one. Note that all packets making up a basic object must have the same token identifier (up to the fifth bit). In Figure 3.4 we have represented an integer that is split up into three packets.
Here is a description of the binary encodings of every kind of OpenMath object:
are encoded depending on how large they
are. There are four possible formats. Integers between -128 and 127 are
encoded as the small integer tags (token
identifier 1) followed by a single byte that is the
value of the integer (interpreted as a signed character). For
example 16 is encoded as 0x01 0x10. Integers between
(
) and
(
) are encoded as
the small integer tag with the long flag set followed by the integer
encoded in four bytes (network byte order:
the most significant byte comes first). For example, 128 is encoded
as 0x81 0x00000080. The most
general encoding begins
with the big integer tag (token identifier 2) with the long flag set
if the number of bytes in the encoding of the digits is greater or
equal than 256. It is followed by the length (in bytes) of the
sequence of digits, encoded on one byte (0 to 255, if the long flag
was not set) or four bytes (network byte order, if the long flag was
set). It is then followed by a byte describing the sign and the
base. This 'sign/base' byte is +
(0x2B) or -
(0x2D) for the sign or-ed with the base mask bits
that can be 0 for base 10
or 0x40 for base 16 or
0x80 for "base 256". It is
followed by the sequence of digits (as
characters for bases 10 and 16 as in the XML
encoding, and as bytes for base 256) in their natural
order. For example, the decimal
number 8589934592
(
) is encoded as
0x02
0x0A 0x2B 0x38 0x35 0x38 0x39 0x39 0x33 0x34 0x35 0x39 0x32
and the
hexadecimal number
xfffffff1 is
encoded as 0x02 0x08
0x6b 0x66 0x66 0x66 0x66 0x66 0x66 0x66 0x31
in the base 16
character encoding and as 0x02 0x04 0xab
0xFF 0xFF 0xFF 0xF1 in the byte encoding (base 256).
Note that it is permitted to encode a "small" integer in any "bigger" format.
To splice sequences of integer packets into integers, we have to consider three cases: In the case of token identifiers 1, 33, and 65 the sequence of packets is treated as a sequence of integer digits to the base of (most significant first). The case of token identifiers 129, 161, and 193 is analogous with digits of base . In the case of token identifiers 2, 34, 66, 130, 162, and 194 the integer is assembled by concatenating the string of decimal digits in the packets in sequence order (which corresponds to most significant first). Note that in all cases only the sequence-initial packet may contain a signed integer. The sign of this packet determines the sign of the overall integer.
| Byte | Hex | Meaning | Byte | Hex | Meaning | |
|---|---|---|---|---|---|---|
| 1 | 22 | begin streamed big integer tag | 7 | 2B | sign + (disregarded) | |
| 2 | FF | 255 digits in packet | 8 | ... | the 255 digits as characters | |
| 3 | 2B | sign + | 9 | 2 | begin final big integer tag | |
| 4 | ... | the 255 digits as characters | 10 | 42 | 68 digits in packet | |
| 5 | 22 | begin streamed big integer tag | 11 | 2B | sign + (disregarded) | |
| 6 | FF | 255 digits in packet | 12 | ... | the 68 digits as characters |
are encoded as the symbol tags
(token identifier 8) with the long flag
set if the maximum of the length in bytes in the UTF-8 encoding of the Content Dictionary name
or the symbol name is greater than or equal to 256. The symbol tag is followed by the
length in bytes in the UTF-8 encoding of the Content Dictionary name, the symbol
name, and the id (if the shared bit was set) as a byte
(if the long flag was not set) or a four byte integer (in network byte
order). These are followed by the bytes of the UTF-8 encoding of the Content
Dictionary name, the symbol name, and the id.
are encoded using the variable tags
(token identifiers 5) with the long
flag set if the number of bytes in the UTF-8 encoding of the variable name is
greater than or equal to 256. Then, there is the number of characters
as a byte (if the long flag was not set) or a four byte integer
(in network byte order), followed by the characters of the name of
the variable. For example, the variable x is encoded as 0x05
0x01 0x78.
are encoded using the floating-point
number tags (token identifier 3) followed by eight bytes that are the IEEE 754
representation [22], most significant bytes first.
For example,
is encoded as 0x03 3ddb7cdfd9d7bdbb.
are encoded in two ways depending on whether the string is encoded in UTF-16 or ISO-8859-1 (LATIN-1). In the case of LATIN-1 it is encoded as the one byte character string tags (token identifier 6) with the long flag set if the number of bytes (characters) in the string is greater than or equal to 256. Then, there is the number of characters as a byte (if the length flag was not set) or a four byte integer (in network byte order), followed by the characters in the string. If the string is encoded in UTF-16, it is encoded as the UTF-16 character string tags (token identifier 7) with the long flag set if the number of characters in the string is greater or equal to 256. Then, there is the number of UTF-16 units, which will be the number of characters unless characters in the higher planes of Unicode are used, as a byte (if the long flag was not set) or a four byte integer (in network byte order), followed by the characters (UTF-16 encoded Unicode).
Sequences of string packets are assumed to have the same encoding for every packet. They are assembled into strings by concatenating the strings in the packets in sequence order.
are encoded using the bytearray tags (token identifier 4) with the long flag set if the number of elements is greater than or equal to 256. Then, there is the number of elements, as a byte (if the long flag was not set) or a four byte integer (in network byte order), followed by the elements of the arrays in their normal order.
Sequences of bytearray packets are assembled into byte arrays by concatenating the bytearrays in the packets in sequence order.
are encoded using the foreign object tags (token identifier 12) with the long flag set if the number of bytes is greater than or equal to 256 and the streaming bit set for dividing it up into packets. Then, there is the number of bytes used to encode the encoding, and the number of bytes used to encode the foreign object. and are represented as a byte (if the long flag was not set) or a four byte integer (in network byte order). These numbers are followed by an -byte representation of the encoding attribute and an byte sequence of bytes encoding the foreign object in their normal order (we call these the payload bytes). The encoding attribute is encoded in UTF-8.
Sequences of foreign object packets are assembled into foreign objects by concatenating the payload bytes in the packets in sequence order.
Note that the foreign object is encoded as a stream of bytes, not a stream of characters. Character based formats (including XML based formats) should be encoded in UTF-8 to produce a stream of bytes to use as the payload of the foreign object.
are encoded using the token identifier 9. The purpose of these
scoping devices is to associate a cdbase with an
object. The start token [9] (or [137] if the long flag is set) is followed
by a single-byte (or 4-byte- if the long flag is set) number
and then by a seqence of
bytes that represent the value of the cdbase
attribute (a URI) in UTF-8 encoding. This is then followed by the binary
encoding of a single object: the object over which this
cdbase attribute has scope.
are encoded using the application tags (token identifiers 16 and 17). More precisely, the application of to … is encoded using the application tags (token identifier 16), the sequence of the encodings of to and the end application tags (token identifier 17).
are encoded using the binding tags (token identifiers 26 and 27). More precisely, the binding by of variables … in is encoded as the binding tag (token identifier 26), followed by the encoding of , followed by the binding variables tags (token identifier 28), followed by the encodings of the variables … , followed by the end binding variables tags (token identifier 29), followed by the encoding of , followed by the end binding tags (token identifier 27).
are encoded using the attribution tags (token identifiers 18 and 19). More precisely, attribution of the object with ( , ), ( , ) pairs (where are the attributes) is encoded as the attributed object tag (token identifier 18), followed by the encoding of the attribute pairs as the attribute pairs tags (token identifier 20), followed by the encoding of each symbol and value, followed by the end attribute pairs tag (token identifier 21), followed by the encoding of , followed by the end attributed object tag (token identifier 19).
are encoded using the error tags (token identifiers 22 and 23). More precisely, applied to … is encoded as the error tag (token identifier 22), the encoding of , the sequence of the encodings of to and the end error tag (token identifier 23).
are encoded using the internal reference tags [30] and [30+128] (the sharing flag cannot be set on this tag, since chains of references are not allowed in the OpenMath binary encoding) with long flag set if the number of OpenMath sub-objects in the encoded OpenMath is greater than or equal to 256. Then, there is the ordinal number of the referenced OpenMath object as a byte (if the long flag was not set) or a four byte integer (in network byte order).
are encoded using the external reference tags [31] and [31+128] (the sharing flag cannot be set on this tag, since chains of references are not allowed in the OpenMath binary encoding) with the long flag set if the number of bytes in the reference URI is greater than or equal to 256. Then, there is the number of bytes in the URI used for the external reference as a byte (if the long flag was not set) or a four byte integer (in network byte order), followed by the URI.
As a simple example of the binary encoding, we can consider the OpenMath object It is binary encoded as the sequence of bytes given in Figure 3.5.
| Byte | Hex | Meaning | Byte | Hex | Meaning | Byte | Hex | Meaning |
|---|---|---|---|---|---|---|---|---|
| 1 | 58 | begin object tag | 19 | 10 | begin application tag | 40 | 10 | begin application tag |
| 2 | 2 | version 2.0 (major) | 20 | 08 | symbol tag | 41 | 48 | symbol tag (with share bit on) |
| 3 | 0 | version 2.0 (minor) | 21 | 06 | cd length | 42 | 01 | reference to second symbol seen (arith1:plus) |
| 4 | 10 | begin application tag | 22 | 04 | name length | 43 | 45 | variable tag (with share bit on) |
| 5 | 08 | symbol tag | 23 | 61 | a (cd name begin | 44 | 00 | reference to first variable seen (x) |
| 6 | 06 | cd length | 24 | 72 | r . | 45 | 05 | variable tag |
| 7 | 05 | name length | 25 | 69 | i . | 46 | 01 | name length |
| 8 | 61 | a (cd name begin | 26 | 74 | t . | 47 | 7a | z (variable name) |
| 9 | 72 | r . | 27 | 68 | h . | 48 | 11 | end application tag |
| 10 | 69 | i . | 28 | 31 | 1 .) | 49 | 11 | end application tag |
| 11 | 74 | t . | 29 | 70 | p (symbol name begin | 50 | 11 | end application tag |
| 12 | 68 | h . | 30 | 6c | l . | |||
| 13 | 31 | 1 .) | 31 | 75 | u . | |||
| 14 | 74 | t (symbol name begin | 32 | 73 | s .) | |||
| 15 | 69 | i . | 33 | 05 | variable tag | |||
| 16 | 6d | m . | 34 | 01 | name length | |||
| 17 | 65 | e . | 35 | 78 | x (name) | |||
| 18 | 73 | s .) | 36 | 05 | variable tag | |||
| 37 | 01 | name length | ||||||
| 38 | 79 | y (variable name) | ||||||
| 39 | 11 | end application tag |
OpenMath 2 introduced a new sharing mechanism, described below. First however we describe the original OpenMath 1 mechanism.
This
form of sharing is deprecated but included for
backwards compatibility with OpenMath 1. It
supports the sharing of symbols, variables and strings
(up to a certain length for strings) within one object. That is, sharing between
objects is not supported. A reference to a shared symbol, variable or string is
encoded as the corresponding tag with the long flag not set and the shared flag
set, followed by a positive integer
encoded as one byte (0
to 255). This integer references the
-th such sharable sub-object (symbol, variable or string up to
255 characters) in the current OpenMath object (counted in the order they are
generated by the encoding). For example, 0x48 0x01
references a symbol that is identical to the second symbol that was found in the
current object. Strings with 8 bit characters and strings with 16 bit characters
are two different kinds of objects for this sharing. Only strings containing less
than 256 characters can be shared (i.e. only strings up to 255 characters).
In the binary encoding specified in the last section (which we keep for compatibility reasons, but deprecate in favor of the more efficient binary encoding specified in this section) only symbols, variables, and short strings could be shared. In this section, we will present a second binary encoding, which shares most of the identifiers with the one in the last one, but handles sharing differently. This encoding is signaled by the shared object tag [88].
The main difference is the interpretation of the sharing flag (bit 7),
which can be set on all objects that allow it. Instead of encoding a reference to a
previous occurrence of an object of the same type, it indicates
whether an object will be referenced later in the encoding. This
corresponds to the information, whether an id
attribute is set
in the XML encoding. On the object identifier (where sharing does not
make sense), the shared flag signifies the encoding described here
([88]=[24+64]).
Otherwise integers, floats, variables, symbols, strings, bytearrays, and constructs are treated exactly as in the binary encoding described in the last section.
The binary encoding with references uses the additional reference tags [30] for (short) internal references, [30+128] for long internal references, [31] for (short) external references, [31+128] for long external references. Internal references are used to share sub-objects in the encoded object (see Figure 3.6 for an example) by referencing their position; external references allow to reference OpenMath objects in other documents by a URI.
Identifiers [30+64] and [30+64+128] are not used, since they would encode references that are shared themselves. Chains of references are redundant, and decrease both space and time efficiency, therefore they are not allowed in the OpenMath binary encoding.
References consist of the identifier [30] ([30+128] for long references)
followed by a positive integer
coded on one byte (4 bytes for long
references). This integer references the
th shared sub-object (one
where the
shared flag is set) in the current object (counted in the order they are generated
in the encoding). For example Ox7E Ox01 references the
second shared sub-object. Figure 3.6 shows the binary
encoding of the object in Figure 3.1
above.
| Byte | Hex | Meaning | Byte | Hex | Meaning | Byte | Hex | Meaning |
|---|---|---|---|---|---|---|---|---|
| 1 | 58 | begin object tag | 12 | 50 | begin application tag (shared) | 23 | 1E | short reference |
| 2 | 2 | version 2.0 (major) | 13 | 05 | variable tag | 24 | 00 | to the first shared object |
| 3 | 0 | version 2.0 (minor) | 14 | 01 | variable length | 25 | 11 | end application tag |
| 4 | 10 | begin application tag | 15 | 66 | f (variable name) | 26 | 1E | short reference |
| 5 | 05 | variable tag | 16 | 05 | variable tag | 27 | 00 | to the second shared object |
| 6 | 01 | variable length | 17 | 01 | variable length | 28 | 11 | end application tag |
| 7 | 66 | f (variable name) | 18 | 61 | a (variable name) | |||
| 8 | 50 | begin application tag (shared) | 19 | 05 | variable tag | |||
| 9 | 05 | variable tag | 20 | 01 | variable length | |||
| 10 | 01 | variable length | 21 | 61 | a (variable name) | |||
| 11 | 66 | f (variable name) | 22 | 11 | end application tag |
It is easy to see that in this binary encoding, the size of the encoding is bytes, where is the depth of the tree, while a totally unshared encoding is bytes (sharing variables saves up to 256 bytes for trees up to depth 8 and wastes space for greater depths). The shared XML encoding only uses bytes, which is more space efficient starting at depth 9.
Note that in the conversion from the XML to the binary encoding the identifiers on the objects are not preserved. Moreover, even though the XML encoding allows references across objects, as in Figure 3.2, the binary encoding does not (the binary encoding has no notion of a multi-object collection, while in the XML encoding this would naturally correspond to e.g. the embedding of multiple OpenMath objects into a single XML document).
Note that objects need not be fully shared (or shared at all) in the binary encoding with sharing.
A typical implementation of the binary encoding comes in two parts. The
first part deals with the unshared encodings, i.e. objects starting with the
identifier [24].
This part uses four tables, each of 256 entries, for symbol, variables, 8 bit character strings whose lengths are less than 256 characters and 16 bit character strings whose lengths are less than 256 characters. When an object is read, all the tables are first flushed. Each time a sharable sub-object is read, it is entered in the corresponding table if it is not full. When a reference to the shared -th object of a given type is read, it stands for the -th entry in the corresponding table. It is an encoding error if the -th position in the table has not already been assigned (i.e. forward references are not allowed). Sharing is not mandatory, there may be duplicate entries in the tables (if the application that wrote the object chose not to share optimally).
The part for the shared representations of OpenMath objects uses an unbounded
array for storing shared sub-objects. Whenever an object has the shared flag
set, then it is read and a pointer to the generated data structure is stored at
the next position of the array. Whenever a reference of the form
[30] [_] is
encountered, the array is queried for the value at [_]
and analogously for [30+128] {_}. Note that the
application can decide to copy the value or share it among sub-terms as long as
it respects the identity conditions given by the tree-nature of the OpenMath
objects. The implementation must take care to ensure that no variables
are captured during this process (see section
Section 3.1.3.2), and possibly have methods for recovering
from cyclic dependency relations (this can be done by standard loop-checking
methods).
Writing an object is simple. The tables are first flushed. Each time a sharable sub-object is encountered (in the natural order of output given by the encoding), it is either entered in the corresponding table (if it is not full) and output in the normal way or replaced by the right reference if it is already present in the table.
The OpenMath 2 binary encoding significantly extends the OpenMath 1 binary encoding to accommodate the new features and in particular sharing of sub-objects. The tags and structure of the OpenMath 1 binary encoding are still present in the current OpenMath binary encoding, so that binary encoded OpenMath 1 objects are still valid in the OpenMath 2 binary encoding and correspond to the same abstract OpenMath objects. In some cases, the binary encoding tags without the shared flag can still be used as more compact representations of the objects (which are not shared, and do not have an identifier).
As the binary encoding is geared towards compactness, OpenMath objects should be constructed so as to maximise internal sharing (if computationally feasible). Note that since sharing is done only at the encoding level, this does not alter the meaning of an OpenMath object, only allows it to be represented more compactly.
The key points of this chapter are:
The XML encoding for OpenMath objects uses most common character sets.
The XML encoding is readable, writable and can be embedded in most documents and transport protocols.
The binary encoding for OpenMath objects should be used when efficiency is a key issue. It is compact yet simple enough to allow fast encoding and decoding of objects.
In this chapter we give a brief overview of Content Dictionaries before explicitly stating their functionality and encoding.
Content Dictionaries (CDs) are central to the OpenMath philosophy of transmitting mathematical information. It is the OpenMath Content Dictionaries which actually hold the meanings of the objects being transmitted.
For example if application is talking to application , and sends, say, an equation involving multiplication of matrices, then and must agree on what a matrix is, and on what matrix multiplication is, and even on what constitutes an equation. All this information is held within some Content Dictionaries which both applications agree upon.
A Content Dictionary holds the meanings of (various) mathematical "words". These words are OpenMath basic objects referred to as symbols in Section 2.1.
With a set of symbol definitions (perhaps from several Content Dictionaries), and can now talk in a common "language".
It is important to stress that it is not Content Dictionaries themselves which are being transmitted, but some "mathematics" whose definitions are held within the Content Dictionaries. This means that the applications must have already agreed on a set of Content Dictionaries which they "understand" (i.e., can cope with to some degree).
In many cases, the Content Dictionaries that an application understands will be constant, and be intrinsic to the application's mathematical use. However the above approach can also be used for applications which can handle every Content Dictionary (such as an OpenMath parser, or perhaps a typesetting system), or alternatively for applications which understand a changeable number of Content Dictionaries (perhaps after being sent Content Dictionaries in some way).
The primary use of Content Dictionaries is thought to be for designers of Phrasebooks, the programs which translate between the OpenMath mathematical object and the corresponding (often internal) structure of the particular application in question. For such a use the Content Dictionaries have themselves been designed to be as readable and precise as possible.
Another possible use for OpenMath Content Dictionaries could rely on their automatic comprehension by a machine (e.g., when given definitions of objects defined in terms of previously understood ones), in which case Content Dictionaries may have to be passed as data. Towards this end, a Content Dictionary has been written which contains a set of symbols sufficient to represent any other Content Dictionary. This means that Content Dictionaries may be passed in the same way as other (OpenMath) mathematical data.
Finally, the syntax of the reference encoding for Content Dictionaries has been designed to be relatively easy to learn and to write, and also free from the need for any specialist software. This is because it is acknowledged that there is an enormous amount of mathematical information to represent, and so most Content Dictionaries are written by "ordinary" mathematicians, encoding their particular fields of expertise. A further reason is that the mathematics conveyed by a specific Content Dictionary should be understandable independently of any application.
The key points from this section are:
Content Dictionaries should be readable and precise to help Phrasebook designers,
Content Dictionaries should be readily write-able to encourage widespread use,
It ought to be possible for a machine to understand a Content Dictionary to some degree.
In this section we define the abstract structure of Content Dictionaries.
A Content Dictionary consists of the following mandatory pieces of information:
A name corresponding to the rules described in Section 2.3.
A description of the Content Dictionary.
A revision date, the date of the last change to the Content Dictionary. Dates should be stored in the ISO-compliant format YYYY-MM-DD, e.g. 1966-02-03.
A review date, a date until which the content dictionary is guaranteed to remain unchanged.
A version number which consists of a major and minor part (see Section 4.2.2).
A status, as described in Section 4.2.1.
A CD base which, when combined with the CD name, forms a unique identifier for the Content Dictionary. It may or may not refer to an actual location from which it can be retrieved.
A series of one or more symbol definitions as described below.
A symbol definition consists of the following pieces of information:
A mandatory name corresponding to the rules described in Section 2.3.
A mandatory description of the symbol, which can be as formal or informal as the author likes.
An optional role as described in Section 2.1.4.
Zero or more commented mathematical properties which are mathematical properties of the symbol expressed in a mechanism other than OpenMath.
Zero or more formal mathematical properties which are mathematical properties of the symbol expressed in OpenMath. Note that it is common for commented and formal mathematical properties to be introduced in pairs, with the former describing the latter.
A Formal Mathematical Property may be given an optional kind attribute. An author of a Content Dictionary may use this to indicate whether, for example, the property provides an algorithm for evaluation of the concept it is associated with. At present no fixed scheme is mandated for how this information should be encoded or used by an application.
Zero or more examples which are intended to demonstrate the use of the symbol within an OpenMath object.
Some pieces of information which might logically be thought to be part of a Content Dictionary, such as the types or signatures of symbols, are better represented externally. This allows for new variants to be associated with Content Dictionaries without the Dictionaries themselves being changed. A model for signatures is given in Section 4.4.1.
Content Dictionaries may be grouped into CD Groups. These groups allow applications to easily refer to collections of Content Dictionaries. One particular CDGroup of interest is the "MathML CDGroup". This group consists of the collection of core Content Dictionaries that is designed to have the same semantic scope as the content elements of MathML [19]. OpenMath objects built from symbols that come from Content Dictionaries in this CDGroup may be expected to be easily transformed between OpenMath and MathML encodings. The detailed structure of a CDGroup is described in Section 4.4.2 below.
The status of a Content Dictionary can be either
official: approved by the OpenMath Society
according to the procedure outlined in Section 4.5;
experimental: under development and thus
liable to change;
private: used by a private group of OpenMath
users;
obsolete: an obsolete Content
Dictionary kept only for archival purposes.
A version number must consist of two parts, a major version and a revision, both of which should be non-negative integers. In CDs that do not have status experimental, the version number should be a positive integer.
Unless a CD has status experimental, no changes should ever be introduced that invalidate objects built with previous versions. Any change that influences phrasebook compliance, like adding a new symbol to a Content Dictionary, is considered a major change and should be reflected by an increase in the major version number. Other changes, like adding an example or correcting a description, are considered minor changes. For minor changes the version number is not changed, but an increase should be made to the revision number. Note that a change such as removing a symbol should not be made unless the CD has status experimental. Should this be required then a new CD with a different name should be produced so as not to invalidate existing objects.
When the major version number is increased, the revision number is normally reset to zero.
As detailed in Chapter 5, OpenMath compliant applications state which versions of which CDs they support.
The reference encoding of Content Dictionaries are as XML documents. A valid Content Dictionary document should conform to the Relax NG Schema for Content Dictionaries given in Section 4.3.1.
An example of a complete Content Dictionary is given in
Appendix Appendix A.1, which is the
Meta Content Dictionary for describing
Content Dictionaries themselves. A more typical Content Dictionary is
given in Appendix A.2, the
arith1 Content Dictionary for basic
arithmetic functions.
# ********************************************* # # Relax NG Schema for OpenMath CD # # ********************************************* default namespace = "http://www.openmath.org/OpenMathCD" include "openmath2.rnc" {start = CD} CDComment = element CDComment { text } CDName = element CDName { xsd:NCName } CDUses = element CDUses { CDName* } CDURL = element CDURL { xsd:anyURI } CDBase = element CDBase { xsd:anyURI } text-or-om = (text | OMOBJ)* CDReviewDate = element CDReviewDate { xsd:date } CDDate = element CDDate { xsd:date } CDVersion = element CDVersion { xsd:nonNegativeInteger } CDRevision = element CDRevision { xsd:nonNegativeInteger } CDStatus = element CDStatus { "official" | "experimental" | "private" | "obsolete"} Description = element Description { text } Name = element Name { xsd:NCName } Role = element Role { "binder" | "attribution" | "semantic-attribution" | "error" | "application" | "constant" } CMP = element CMP { text } FMP = element FMP { attribute kind {xsd:string}?, OMOBJ } # allow embedded OM Example = element Example { text-or-om } CDDefinition = element CDDefinition { CDComment*, (Name & Role? & Description), (CDComment | Example | FMP | CMP)* } CD = element CD { (CDComment* & Description? & CDName & CDURL? & CDBase? & CDReviewDate? & CDDate & CDStatus & CDUses? & CDVersion & CDRevision), ( CDDefinition,CDComment* )+ }
We now describe the elements used in the above schema in terms of the abstract description of CDs in Section 4.2. Unless stated otherwise information is encoded as the content of the relevant element.
CDNameThe name of the Content Dictionary.
DescriptionThe text occurring in the Description
element is used to give a description of the enclosing element, which
could be a symbol or the entire Content Dictionary. The content of
this element can be any XML text.
CDReviewDateThe review date of the Content Dictionary.
CDDateThe revision date of this version of the Content Dictionary.
CDVersionThe major version number of the CD.
CDRevisionThe minor version number of the CD.
CDStatusThe status of the Content Dictionary.
CDBaseThe CD base of the CD.
CDURLThe
text occurring in the CDURL element should
be a valid URL where the source file for the Content Dictionary
encoding can be found (if it exists). The filename should conform to
ISO 9660 [11].
CDUsesThe content of this element should
be a series of CDName elements, each
naming a Content Dictionary used in the
Example and FMPs
of the current Content Dictionary. This element is optional and deprecated since
the information can easily be extracted automatically.
CDCommentThe content of this element should be text that does not convey any crucial information concerning the current Content Dictionary. It can be used in the Content Dictionary header to report the author of the Content Dictionary and to log change information. In the body of the Content Dictionary, it can be used to attach extra remarks to certain symbols.
CDDefinitionThe element which contains the definition of an individual symbol.
NameThe name of a symbol.
RoleThe role of a symbol: it must be one of binder, attribution, semantic-attribution, error, application, or constant.
ExampleThe text occurring in the
Example element is used to give examples of
the enclosing symbol, and can be any XML text. In addition to text
the element may contain examples as XML encoded OpenMath, inside
OMOBJ elements. Note that
Examples must be with respect to some symbol
and cannot be "loose" in the Content Dictionary.
CMPA Commented Mathematical Property.
FMP
A Formal Mathematical Property. It may take an optional
kind attribute.
Content Dictionaries contain just one part of the information that can be associated to a symbol in order to define its meaning and its functionality. OpenMath Signature dictionaries, CDGroups, and possibly collections of extra mathematical properties, are used to convey the different aspects that as a whole make up a mathematical definition.
OpenMath may be used with any type system. One just needs to produce a Content Dictionary which gives the constructors of the type system, and then one may build OpenMath objects representing types in the given type system. These are typically associated with OpenMath objects via the OpenMath attribution constructor.
A Small Type System, called STS, has been designed to give semi-formal signatures to OpenMath symbols and is documented in [5]. The signature file given in Appendix A.3 is based on this formalism. Using the same mechanism, [4] shows how pure type systems can also be employed to assign types to OpenMath symbols.
Signature dictionaries have a header which specifies the type system being used and the Content Dictionary containing the symbols for which signatures are being given. Each signature takes the form of an OpenMath object in an appropriate encoding.
A type definition: the name of the Content Dictionary or of the CDGroup (cfg. Section 4.4.2) that represents the type system being used.
A CD name: the name of the CD for which signatures are being defined.
A review date as defined in Section 4.2.
A status: as defined in Section 4.2.
A series of signatures which are OpenMath objects in some encoding. The objects must represent types as defined by the type definition.
The following is a reference encoding of a signature dictionary, designed to be used with Content Dictionaries in the XML encoding.
# ********************************************* # # Relax NG Schema for OpenMath CD Signatures # # ********************************************* default namespace = "http://www.openmath.org/OpenMathCDS" include "openmath2.rnc" { start = CDSignatures } CDSComment = element CDSComment { text } CDSReviewDate = element CDSReviewDate { text } CDSStatus = element CDSStatus { "official" | "experimental" | "private" | "obsolete"} CDSignatures = element CDSignatures { attlist.CDSignatures, (CDSComment)*, (CDSReviewDate? & CDSStatus), (CDSComment | Signature)* } attlist.CDSignatures = attribute cd { xsd:NCName }, attribute type { xsd:NCName } Signature = element Signature { attlist.Signature, OMOBJ? } attlist.Signature = attribute name { text }
An example of a signature dictionary for the type system STS and the
arith1 Content Dictionary is given in Appendix A.3. Each signature entry is similar to the
following one for the OpenMath symbol <OMS cd="arith1"
name="plus"/>:
<Signature name="plus"> <OMOBJ version="2.0"> <OMA> <OMS name="mapsto" cd="sts"/> <OMA> <OMS name="nassoc" cd="sts"/> <OMV name="AbelianSemiGroup"/> </OMA> <OMV name="AbelianSemiGroup"/> </OMA> </OMOBJ> </Signature>
The CD Group mechanism is a convenience mechanism for identifying collections of CDs. A CD Group file is an XML document used in the (static or dynamic) negotiation phase where communicating applications declare and agree on the Content Dictionaries which they process. It is a complement, or an alternative, to the individual declaration of Content Dictionaries understood by an application. Note that CD Groups do not affect the OpenMath objects themselves. Symbols in an object always refer to content dictionaries, not groups.
For an application to declare that it "understands CDGroup G" is exactly equivalent to, and interchangeable with, the declaration that it "understands Content Dictionaries , , … ", where , … are the members of CDGroup G.
CDGroups are XML documents, hence a valid CDGroup should
be valid according to the schema given in Figure 4.1,
adhere to the extra conditions on the content of the elements given in Section 4.4.2.2.
Apart from some header information such as CDGroupName and
CDGroup version, a CDGroup is simply an unordered list of
CDs, identified by name and optionally version number and URL.
# Schema for OpenMath CD groups # info on the CD group itself default namespace = "http://www.openmath.org/OpenMathCDG" CDGroupName = element CDGroupName { xsd:NCName } CDGroupVersion = element CDGroupVersion { xsd:nonNegativeInteger } CDGroupRevision = element CDGroupRevision { xsd:nonNegativeInteger } CDGroupURL = element CDGroupURL { text } CDGroupDescription = element CDGroupDescription { text } # info on the CDs in the group CDComment = element CDComment { text } CDGroupMember = element CDGroupMember { CDComment?, CDName, CDVersion?, CDURL? } CDName = element CDName { xsd:NCName } CDVersion = element CDVersion { xsd:nonNegativeInteger } CDURL = element CDURL { text } # structure of the group CDGroup = element CDGroup { CDGroupName, CDGroupVersion, CDGroupRevision?, CDGroupURL, CDGroupDescription, (CDGroupMember | CDComment)* } start = CDGroup
The notion of being a valid CDGroup implies that the following requirements on the content of the elements described by the schema given in Section 4.4.1.2 are also met.
CDGroupThe XML element CDGroup is the outermost
element in a CDGroup document.
CDGroupNameThe text occurring in the CDGroupName
element corresponds to the name of the CDGroup. For the syntactical
requirements, see CDName in Section 4.3.2.
CDGroupVersionCDGroupRevisionThe text occurring in these elements contains the major and minor version numbers of the CDGroup.
CDGroupURLThe text occurring in the CDGroupURL
element identifies the location of the CDGroup file, not necessarily
of the member Content Dictionaries. For the syntactical
requirements, see CDURL in Section 4.3.2.
CDGroupDescriptionThe text occurring in the
CDGroupDescription element describes the
mathematical area of the CDGroup.
CDGroupMemberThe XML element CDGroupMember
encloses the data identifying each member of the CDGroup.
CDNameThe
text occurring in the CDName element
corresponds to the name of a Content Dictionary in the CDGroup. For
the syntactical requirements, see CDName in
Section 4.3.2.
CDVersionThe
text occurring in the CDVersion element
identifies which version of the Content Dictionary is to be taken as
member of the CDGroup. This element is optional. In case it is
missing, the latest version is the one included in the CDGroup. For
the syntactical requirements, see CDVersion
in Section 4.3.2.
CDURLThe text occurring in the CDURL element
identifies the location of the Content Dictionary to be taken as
member of the CDGroup. This element is optional. In case it is
missing, the location of the CDGroup identified by the element
CDGroupURL is assumed. For the syntactical
requirements, see CDURL in Section 4.3.2.
CDCommentSee
CDComment in Section 4.3.2.
The OpenMath Society is responsible for implementing a
review and referee process to assess the accuracy of the mathematical
content of Content Dictionaries. The status (see CDStatus)
and/or the version number (see CDVersion ) of a Content
Dictionary may change as a result of this review process.
Applications that meet the requirements specified in this chapter may label themselves as OpenMath compliant. OpenMath compliance is defined so as to maximize the potential for interoperability amongst OpenMath applications.
This standard defines two reference encodings for OpenMath, the binary encoding and XML encoding, defined in Chapter 3.
As a minimum, an OpenMath compliant application, which accepts or generates OpenMath objects, must be capable of doing so using the XML encoding. The ability to use other encodings is optional.
All OpenMath objects generated by a compliant OpenMath application must validate against the Relax NG Schema given in Appendix B.
In the XML encoding, floating-point numbers may be defined using either decimal or hexadecimal notation. For numerical values, plus the two infinities, the two representations may be used interchangeably since there is a one-to-one correspondence between them. The exceptional case is that of not a number (NaN) which is defined in the IEEE standard [22] to be any number whose exponent has the maximum possible value (in this case the exponent is 11 bits so the maximum value is 2047) and whose mantissa is non-zero. The standard explicitly notes the use of the 52 bits in the mantissa (and also the sign bit) to store information about how the NaN was generated in a system-specific way. Thus in some cases the exact representation of the NaN is significant.
The semantics of the OpenMath object
<OMF dec="NaN"/> is that it represents
any NaN, and a phrasebook may substitute any
specific NaN value when processing it. The semantics of a NaN in
hexadecimal notation however, such as
<OMF hex="FFF8000000000001"/>,
is that this is a specific NaN, as distinct from all others.
If a phrasebook author substitutes
another value for the NaN or maps all NaNs to a single object then he or
she must recognise that this process is not an identity transformation.
An OpenMath Foreign Object may be attributed with a string indicating the format of its contents. Although this information is optional, an OpenMath-compliant application which generates OpenMath Foreign Objects should always include it where possible (see the discussion of MathML conversion below for an example of a situation where it is not always possible). It is recommended that, where the contents of the Foreign Object are in an XML dialect, the namespace [14] of the XML dialect is used as the value of the encoding. For example (using the XML encoding):
<OMATTR>
<OMATP>
<OMS cd="annotations1" name="description"/>
<OMFOREIGN encoding="http://www.w3.org/1999/xhtml">
<html xmlns="http://www.w3.org/1999/xhtml">
<head><title>E</title></head>
<body>
<p>
The base of the natural logarithms, approximately 2.71828.
</p>
</body>
</html>
</OMFOREIGN>
</OMATP>
<OMS cd="nums1" name="e"/>
</OMATTR>Where the contents of the Foreign Object is a format other than XML, it is recommended that its MIME type [3] is used as the value of the encoding. For example (again using the XML encoding):
<OMATTR>
<OMATP>
<OMS cd="annotations1" name="description"/>
<OMFOREIGN encoding="text/latex">
\documentclass{article}
\begin{document}
\title{E}
\maketitle
The base of the natural logarithms, approximately 2.71828.
\end{document}
</OMFOREIGN>
</OMATP>
<OMS cd="nums1" name="e"/>
</OMATTR> An exception to the above guidelines occurs when a MathML object
is converted to OpenMath. MathML also has an
encoding attribute which can appear in various
places and whose format is a string. Only two values are predefined,
MathML-Content and
MathML-Presentation, and these may appear in
the resulting OpenMath object despite the fact that they are not namespaces
as recommended above. For example the following MathML expression:
<semantics xmlns="http://www.w3.org/1998/Math/MathML">
<apply>
<sin/>
<ci>x</ci>
</apply>
<annotation encoding="MathML-Presentation">
<math>
<mi>sin</mi><mfenced><mi>x</mi></mfenced>
</math>
</annotation>
</semantics>is equivalent to the OpenMath expression:
<OMATTR>
<OMATP>
<OMS cd="altenc" name="MathML_encoding"/>
<OMFOREIGN encoding="MathML-Presentation">
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mi>sin</mi><mfenced><mi>x</mi></mfenced>
</math>
</OMFOREIGN>
</OMATP>
<OMA>
<OMS cd="transc1" name="sin"/>
<OMV name="x"/>
</OMA>
</OMATTR>
Since in MathML the encoding attribute is in
effect optional (its default value is the empty string), a convertor
program may not in fact be able to provide a value for the OpenMath
encoding attribute. This is unfortunate but
unavoidable.
An OpenMath compliant application must be able to support the error Content Dictionary defined in Appendix A.5.
A compliant application must declare the names and version numbers of
the Content Dictionaries that it supports. Equivalently it may declare
the Content Dictionary Group (or groups) and major version number (not
revision number), rather than listing individual Content Dictionaries.
Applications that support all Content Dictionaries (e.g. renderers)
should refer to the implicit CD Group all.
If a compliant application supports a Content Dictionary then it must explicitly declare any symbols in the Content Dictionaries that are not supported. Phrasebooks are encouraged to support every symbol in the Content Dictionaries.
Symbols which are not listed as unsupported are supported by the application. The meaning of supported will depend on the application domain. For example an OpenMath renderer should provide a default display for any OpenMath object that only references supported symbols, whereas a Computer Algebra System will be expected to map such an object to a suitable internal representation, in this system, of this mathematical object. It is expected that the application's phrasebooks for supported Content Dictionaries will be constructed such that properties of the symbol expressed in the Content Dictionary are respected as far as possible for the given application domain. However OpenMath compliance does not imply any guarantee by the OpenMath Society on the accuracy of these representations.
Content Dictionaries available from the official OpenMath repository
at www.openmath.org need only be referenced by name, other Content
Dictionaries should be referenced using the
CDBase and the
CDName.
When receiving an OpenMath symbol, e.g.
,
that is not defined in
a supported Content Dictionary, a
compliant application will act as if it had received the OpenMath object
where
unhandled_symbol is the symbol from the
error Content Dictionary.
Similarly if it receives a symbol, e.g. , from an unsupported Content Dictionary, it will act as if it had received the OpenMath object
Finally if the compliant application receives a symbol from a supported Content Dictionary but with an unknown name, then this must either be an incorrect object, or possibly the object has been built using a later version of the Content Dictionary. In either case, the application will act as if it had received the OpenMath object
The previous section defines the behaviour of a compliant application upon receiving well formed OpenMath objects containing unexpected symbols. This standard does not specify any behaviour for an application upon receiving ill-formed objects.
Compliant OpenMath 2 documents and Content Dictionary files using the
reference XML encodings must be valid
according to the specified schema, and so will use the namespaces
http://www.openmath.org/OpenMath
and
http://www.openmath.org/OpenMathCD
respectively. Similarly CD Group and Signature files will use
http://www.openmath.org/OpenMathCDG
and
http://www.openmath.org/OpenMathCDS.
Applications may also support OpenMath 1.
XML-encoded OpenMath 1 documents may be in either the
http://www.openmath.org/OpenMath
namespace or in no-namespace (i.e., do not have any xmlns
declarations).
An application may accept either of
these forms. Note however that OpenMath documents that have a version attribute
should validate against the schema for OpenMath 2 (or later versions) and
so should always use the OpenMath namespace.
XML-encoded OpenMath 1 CD files, CD Group files and CD Signature
files must be in no-namespace. An OpenMath 2 application may support
these files by implicitly converting the documents to their respective
namespace. Apart from this change of namespace (and the addition of a
version attribute on OMOBJ) the OpenMath 1
documents should conform to the schema specified in this standard.
The use of documents in no-namespace should be restricted to reading existing OpenMath 1 files. No OpenMath 2 application should generate documents in this form.
<CD xmlns="http://www.openmath.org/OpenMathCD"> <CDComment> This document is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. The copyright holder grants you permission to redistribute this document freely as a verbatim copy. Furthermore, the copyright holder permits you to develop any derived work from this document provided that the following conditions are met. a) The derived work acknowledges the fact that it is derived from this document, and maintains a prominent reference in the work to the original source. b) The fact that the derived work is not the original OpenMath document is stated prominently in the derived work. Moreover if both this document and the derived work are Content Dictionaries then the derived work must include a different CDName element, chosen so that it cannot be confused with any works adopted by the OpenMath Society. In particular, if there is a Content Dictionary Group whose name is, for example, `math' containing Content Dictionaries named `math1', `math2' etc., then you should not name a derived Content Dictionary `mathN' where N is an integer. However you are free to name it `private_mathN' or some such. This is because the names `mathN' may be used by the OpenMath Society for future extensions. c) The derived work is distributed under terms that allow the compilation of derived works, but keep paragraphs a) and b) intact. The simplest way to do this is to distribute the derived work under the OpenMath license, but this is not a requirement. If you have questions about this license please contact the OpenMath society at http://www.openmath.org. </CDComment> <CDName> meta </CDName> <CDReviewDate>2006-03-30</CDReviewDate> <CDDate>2004-03-30</CDDate> <CDVersion>3</CDVersion> <CDRevision>0</CDRevision> <CDStatus> official </CDStatus> <CDURL> http://www.openmath.org/cd/meta.ocd </CDURL> <CDBase>http://www.openmath.org/cd</CDBase> <Description> This is a content dictionary to represent content dictionaries, so that they may be passed between OpenMath compliant application in a similar way to mathematical objects. The information written here is taken from chapter 4 of the current draft of the "OpenMath Standard". </Description> <CDDefinition> <Name> CD </Name> <Role>application</Role> <Description> The top level element for the Content Dictionary. It just acts as a container for the elements described below. </Description> </CDDefinition> <CDDefinition> <Name> CDDefinition </Name> <Role>application</Role> <Description> This symbol is used to represent the element which contains the definition of each symbol in a content dictionary. That is: it must contain a 'Name' element and a 'Description' element, and it may contain an arbitrary number of 'Example', 'FMP' or 'CMP' elements. </Description> </CDDefinition> <CDDefinition> <Name> CDName </Name> <Role>application</Role> <Description> An element which contains the string corresponding to the name of the CD. The string must match the syntax for CD names given in the OpenMath Standard. Here and elsewhere white space occurring at the beginning or end of the string will be ignored. </Description> </CDDefinition> <CDDefinition> <Name> CDURL </Name> <Role>application</Role> <Description> An optional element. If it is used it contains a string representing the URL where the canonical reference copy of this CD is stored. </Description> </CDDefinition> <CDDefinition> <Name> CDBase </Name> <Role>application</Role> <Description> An optional element. If it is used it contains a string representing the URI to be used as the base for generated canonical URI references for symbols in the CD. </Description> </CDDefinition> <CDDefinition> <Name> Example </Name> <Role>application</Role> <Description> An element which contains an arbitrary number of children, each of which is either a string or an OpenMath Object. These children give examples in natural language, or in OpenMath, of the enclosing symbol definition. </Description> </CDDefinition> <CDDefinition> <Name> CDDate </Name> <Role>application</Role> <Description> An element which contains a date as a string in the ISO-8601 YYYY-MM-DD format. This gives the date at which the Content Dictionary was last edited. </Description> </CDDefinition> <CDDefinition> <Name> CDVersion </Name> <Role>application</Role> <Description> An element which contains a version number for the CD. This should be a non negative integer. Any change to the CD that affects existing OpenMath applications that support this CD should result in an increase in the version number. </Description> </CDDefinition> <CDDefinition> <Name> CDRevision </Name> <Role>application</Role> <Description> An element which contains a revision number (or minor version number) This should be a non-negative integer starting from zero for each new version. Additional examples would be typical changes to a CD requiring a new revision number. </Description> </CDDefinition> <CDDefinition> <Name> CDReviewDate </Name> <Role>application</Role> <Description> An element which contains a date as a string in the ISO-8601 YYYY-MM-DD format. This gives the date at which the Content Dictionary is next scheduled for review. It should be expected to be stable until at least this date. </Description> </CDDefinition> <CDDefinition> <Name> CDStatus </Name> <Role>application</Role> <Description> An element giving information on the status of the CD. The content of the element must be one of the following strings. official (approved by the OpenMath Society), experimental (currently being tested), private (used by a private group of OpenMath users), or obsolete (an obsolete CD kept only for archival purposes). </Description> </CDDefinition> <CDDefinition> <Name> CDComment </Name> <Role>application</Role> <Description> This symbol is used to represent the element of a content dictionary which explains some aspect of that content dictionary. It should have one string argument which makes that explanation. </Description> </CDDefinition> <CDDefinition> <Name> CDUses </Name> <Role>application</Role> <Description> An element which contains zero or more CDNames which correspond to the CDs that this CD depends on, i.e. uses in examples and FMPs. If the CD is dependent on any other CDs they may be present here. </Description> </CDDefinition> <CDDefinition> <Name> Description </Name> <Role>application</Role> <Description> An element which contains a string corresponding to the description of either the CD or the symbol (depending on which is the enclosing element). </Description> </CDDefinition> <CDDefinition> <Name> Name </Name> <Role>application</Role> <Description> An element containing the string corresponding to the name of the symbol being defined. This must match the syntax for symbol names given in the OpenMath Standard. Here and elsewhere white space occurring at the begining or end of the string will be ignored. </Description> </CDDefinition> <CDDefinition> <Name> Role </Name> <Role>application</Role> <Description> An element containing the string corresponding to the role of the symbol being defined. </Description> </CDDefinition> <CDDefinition> <Name> CMP </Name> <Role>application</Role> <Description> An optional element (which may be repeated many times) which contains a string corresponding to a property of the symbol being defined. </Description> </CDDefinition> <CDDefinition> <Name> FMP </Name> <Role>application</Role> <Description> An optional element which contains an OpenMath Object. This corresponds to a property of the symbol being defined. </Description> </CDDefinition> </CD>
<CD xmlns="http://www.openmath.org/OpenMathCD"> <CDComment> This document is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. The copyright holder grants you permission to redistribute this document freely as a verbatim copy. Furthermore, the copyright holder permits you to develop any derived work from this document provided that the following conditions are met. a) The derived work acknowledges the fact that it is derived from this document, and maintains a prominent reference in the work to the original source. b) The fact that the derived work is not the original OpenMath document is stated prominently in the derived work. Moreover if both this document and the derived work are Content Dictionaries then the derived work must include a different CDName element, chosen so that it cannot be confused with any works adopted by the OpenMath Society. In particular, if there is a Content Dictionary Group whose name is, for example, `math' containing Content Dictionaries named `math1', `math2' etc., then you should not name a derived Content Dictionary `mathN' where N is an integer. However you are free to name it `private_mathN' or some such. This is because the names `mathN' may be used by the OpenMath Society for future extensions. c) The derived work is distributed under terms that allow the compilation of derived works, but keep paragraphs a) and b) intact. The simplest way to do this is to distribute the derived work under the OpenMath license, but this is not a requirement. If you have questions about this license please contact the OpenMath society at http://www.openmath.org. </CDComment> <CDName> arith1 </CDName> <CDBase>http://www.openmath.org/cd</CDBase> <CDURL> http://www.openmath.org/cd/arith1.ocd </CDURL> <CDReviewDate>2006-03-30</CDReviewDate> <CDStatus> official </CDStatus> <CDDate>2004-03-30</CDDate> <CDVersion>3</CDVersion> <CDRevision>0</CDRevision> <Description> This CD defines symbols for common arithmetic functions. </Description> <CDDefinition> <Name> lcm </Name> <Role>application</Role> <Description> The symbol to represent the n-ary function to return the least common multiple of its arguments. </Description> <CMP> lcm(a,b) = a*b/gcd(a,b) </CMP> <FMP> <OMOBJ xmlns="http://www.openmath.org/OpenMath" version="2.0" cdbase="http://www.openmath.org/cd"> <OMA> <OMS cd="relation1" name="eq"/> <OMA> <OMS cd="arith1" name="lcm"/> <OMV name="a"/> <OMV name="b"/> </OMA> <OMA> <OMS cd="arith1" name="divide"/> <OMA> <OMS cd="arith1" name="times"/> <OMV name="a"/> <OMV name="b"/> </OMA> <OMA> <OMS cd="arith1" name="gcd"/> <OMV name="a"/> <OMV name="b"/> </OMA> </OMA> </OMA> </OMOBJ> </FMP> <CMP> for all integers a,b | There does not exist a c>0 such that c/a is an Integer and c/b is an Integer and lcm(a,b) > c. </CMP> <FMP> <OMOBJ xmlns="http://www.openmath.org/OpenMath" version="2.0" cdbase="http://www.openmath.org/cd"> <OMBIND> <OMS cd="quant1" name="forall"/> <OMBVAR> <OMV name="a"/> <OMV name="b"/> </OMBVAR> <OMA> <OMS cd="logic1" name="implies"/> <OMA> <OMS cd="logic1" name="and"/> <OMA> <OMS cd="set1" name="in"/> <OMV name="a"/> <OMS cd="setname1" name="Z"/> </OMA> <OMA> <OMS cd="set1" name="in"/> <OMV name="b"/> <OMS cd="setname1" name="Z"/> </OMA> </OMA> <OMA> <OMS cd="logic1" name="not"/> <OMBIND> <OMS cd="quant1" name="exists"/> <OMBVAR> <OMV name="c"/> </OMBVAR> <OMA> <OMS cd="logic1" name="and"/> <OMA> <OMS cd="relation1" name="gt"/> <OMV name="c"/> <OMI>0</OMI> </OMA> <OMA> <OMS cd="integer1" name="factorof"/> <OMV name="a"/> <OMV name="c"/> </OMA> <OMA> <OMS cd="integer1" name="factorof"/> <OMV name="b"/> <OMV name="c"/> </OMA> <OMA> <OMS cd="relation1" name="lt"/> <OMV name="c"/> <OMA> <OMS cd="arith1" name="lcm"/> <OMV name="a"/> <OMV name="b"/> </OMA> </OMA> </OMA> </OMBIND> </OMA> </OMA> </OMBIND> </OMOBJ> </FMP> </CDDefinition> <CDDefinition> <Name> gcd </Name> <Role>application</Role> <Description> The symbol to represent the n-ary function to return the gcd (greatest common divisor) of its arguments. </Description> <CMP> for all integers a,b | There does not exist a c such that a/c is an Integer and b/c is an Integer and c > gcd(a,b). Note that this implies that gcd(a,b) > 0 </CMP> <FMP> <OMOBJ xmlns="http://www.openmath.org/OpenMath" version="2.0" cdbase="http://www.openmath.org/cd"> <OMBIND> <OMS cd="quant1" name="forall"/> <OMBVAR> <OMV name="a"/> <OMV name="b"/> </OMBVAR> <OMA> <OMS cd="logic1" name="implies"/> <OMA> <OMS cd="logic1" name="and"/> <OMA> <OMS cd="set1" name="in"/> <OMV name="a"/> <OMS cd="setname1" name="Z"/> </OMA> <OMA> <OMS cd="set1" name="in"/> <OMV name="b"/> <OMS cd="setname1" name="Z"/> </OMA> </OMA> <OMA> <OMS cd="logic1" name="not"/> <OMBIND> <OMS cd="quant1" name="exists"/> <OMBVAR> <OMV name="c"/> </OMBVAR> <OMA> <OMS cd="logic1" name="and"/> <OMA> <OMS cd="set1" name="in"/> <OMA> <OMS cd="arith1" name="divide"/> <OMV name="a"/> <OMV name="c"/> </OMA> <OMS cd="setname1" name="Z"/> </OMA> <OMA> <OMS cd="set1" name="in"/> <OMA> <OMS cd="arith1" name="divide"/> <OMV name="b"/> <OMV name="c"/> </OMA> <OMS cd="setname1" name="Z"/> </OMA> <OMA> <OMS cd="relation1" name="gt"/> <OMV name="c"/> <OMA> <OMS cd="arith1" name="gcd"/> <OMV name="a"/> <OMV name="b"/> </OMA> </OMA> </OMA> </OMBIND> </OMA> </OMA> </OMBIND> </OMOBJ> </FMP> <Example> gcd(6,9) = 3 <OMOBJ xmlns="http://www.openmath.org/OpenMath" version="2.0" cdbase="http://www.openmath.org/cd"> <OMA> <OMS cd="relation1" name="eq"/> <OMA> <OMS cd="arith1" name="gcd"/> <OMI> 6 </OMI> <OMI> 9 </OMI> </OMA> <OMI> 3 </OMI> </OMA> </OMOBJ> </Example> </CDDefinition> <CDDefinition> <Name> plus </Name> <Role>application</Role> <Description> The symbol representing an n-ary commutative function plus. </Description> <CMP> for all a,b | a + b = b + a </CMP> <FMP> <OMOBJ xmlns="http://www.openmath.org/OpenMath" version="2.0" cdbase="http://www.openmath.org/cd"> <OMBIND> <OMS cd="quant1" name="forall"/> <OMBVAR> <OMV name="a"/> <OMV name="b"/> </OMBVAR> <OMA> <OMS cd="relation1" name="eq"/> <OMA> <OMS cd="arith1" name="plus"/> <OMV name="a"/> <OMV name="b"/> </OMA> <OMA> <OMS cd="arith1" name="plus"/> <OMV name="b"/> <OMV name="a"/> </OMA> </OMA> </OMBIND> </OMOBJ> </FMP> </CDDefinition> <CDDefinition> <Name> unary_minus </Name> <Role>application</Role> <Description> This symbol denotes unary minus, i.e. the additive inverse. </Description> <CMP> for all a | a + (-a) = 0 </CMP> <FMP> <OMOBJ xmlns="http://www.openmath.org/OpenMath" version="2.0" cdbase="http://www.openmath.org/cd"> <OMBIND> <OMS cd="quant1" name="forall"/> <OMBVAR> <OMV name="a"/> </OMBVAR> <OMA> <OMS cd="relation1" name="eq"/> <OMA> <OMS cd="arith1" name="plus"/> <OMV name="a"/> <OMA> <OMS cd="arith1" name="unary_minus"/> <OMV name="a"/> </OMA> </OMA> <OMS cd="alg1" name="zero"/> </OMA> </OMBIND> </OMOBJ> </FMP> </CDDefinition> <CDDefinition> <Name> minus </Name> <Role>application</Role> <Description> The symbol representing a binary minus function. This is equivalent to adding the additive inverse. </Description> <CMP> for all a,b | a - b = a + (-b) </CMP> <FMP> <OMOBJ xmlns="http://www.openmath.org/OpenMath" version="2.0" cdbase="http://www.openmath.org/cd"> <OMBIND> <OMS cd="quant1" name="forall"/> <OMBVAR> <OMV name="a"/> <OMV name="b"/> </OMBVAR> <OMA> <OMS cd="relation1" name="eq"/> <OMA> <OMS cd="arith1" name="minus"/> <OMV name="a"/> <OMV name="b"/> </OMA> <OMA> <OMS cd="arith1" name="plus"/> <OMV name="a"/> <OMA> <OMS cd="arith1" name="unary_minus"/> <OMV name="b"/> </OMA> </OMA> </OMA> </OMBIND> </OMOBJ> </FMP> </CDDefinition> <CDDefinition> <Name> times </Name> <Role>application</Role> <Description> The symbol representing an n-ary multiplication function. </Description> <Example> <OMOBJ xmlns="http://www.openmath.org/OpenMath" version="2.0" cdbase="http://www.openmath.org/cd"> <OMA> <OMS cd="relation1" name="eq"/> <OMA> <OMS cd="arith1" name="times"/> <OMA> <OMS cd="linalg2" name="matrix"/> <OMA> <OMS cd="linalg2" name="matrixrow"/> <OMI> 1 </OMI> <OMI> 2 </OMI> </OMA> <OMA> <OMS cd="linalg2" name="matrixrow"/> <OMI> 3 </OMI> <OMI> 4 </OMI> </OMA> </OMA> <OMA> <OMS cd="linalg2" name="matrix"/> <OMA> <OMS cd="linalg2" name="matrixrow"/> <OMI> 5 </OMI> <OMI> 6 </OMI> </OMA> <OMA> <OMS cd="linalg2" name="matrixrow"/> <OMI> 7 </OMI> <OMI> 8 </OMI> </OMA> </OMA> </OMA> <OMA> <OMS cd="linalg2" name="matrix"/> <OMA> <OMS cd="linalg2" name="matrixrow"/> <OMI> 19 </OMI> <OMI> 22 </OMI> </OMA> <OMA> <OMS cd="linalg2" name="matrixrow"/> <OMI> 43 </OMI> <OMI> 50 </OMI> </OMA> </OMA> </OMA> </OMOBJ> </Example> <CMP> for all a,b | a * 0 = 0 and a * b = a * (b - 1) + a </CMP> <FMP><OMOBJ xmlns="http://www.openmath.org/OpenMath" version="2.0" cdbase="http://www.openmath.org/cd"> <OMBIND> <OMS cd="quant1" name="forall"/> <OMBVAR> <OMV name="a"/> <OMV name="b"/> </OMBVAR> <OMA> <OMS cd="logic1" name="and"/> <OMA> <OMS cd="relation1" name="eq"/> <OMA> <OMS cd="arith1" name="times"/> <OMV name="a"/> <OMS cd="alg1" name="zero"/> </OMA> <OMS cd="alg1" name="zero"/> </OMA> <OMA> <OMS cd="relation1" name="eq"/> <OMA> <OMS cd="arith1" name="times"/> <OMV name="a"/> <OMV name="b"/> </OMA> <OMA> <OMS cd="arith1" name="plus"/> <OMA> <OMS cd="arith1" name="times"/> <OMV name="a"/> <OMA> <OMS cd="arith1" name="minus"/> <OMV name="b"/> <OMS cd="alg1" name="one"/> </OMA> </OMA> <OMV name="a"/> </OMA> </OMA> </OMA> </OMBIND> </OMOBJ></FMP> <CMP> for all a,b,c | a*(b+c) = a*b + a*c </CMP> <FMP><OMOBJ xmlns="http://www.openmath.org/OpenMath" version="2.0" cdbase="http://www.openmath.org/cd"> <OMBIND> <OMS cd="quant1" name="forall"/> <OMBVAR> <OMV name="a"/> <OMV name="b"/> <OMV name="c"/> </OMBVAR> <OMA> <OMS cd="relation1" name="eq"/> <OMA> <OMS cd="arith1" name="times"/> <OMV name="a"/> <OMA> <OMS cd="arith1" name="plus"/> <OMV name="b"/> <OMV name="c"/> </OMA> </OMA> <OMA> <OMS cd="arith1" name="plus"/> <OMA> <OMS cd="arith1" name="times"/> <OMV name="a"/> <OMV name="b"/> </OMA> <OMA> <OMS cd="arith1" name="times"/> <OMV name="a"/> <OMV name="c"/> </OMA> </OMA> </OMA> </OMBIND> </OMOBJ></FMP> </CDDefinition> <CDDefinition> <Name> divide </Name> <Role>application</Role> <Description> This symbol represents a (binary) division function denoting the first argument right-divided by the second, i.e. divide(a,b)=a*inverse(b). It is the inverse of the multiplication function defined by the symbol times in this CD. </Description> <CMP> whenever not(a=0) then a/a = 1 </CMP> <FMP> <OMOBJ xmlns="http://www.openmath.org/OpenMath" version="2.0" cdbase="http://www.openmath.org/cd"> <OMBIND> <OMS cd="quant1" name="forall"/> <OMBVAR> <OMV name="a"/> </OMBVAR> <OMA> <OMS cd="logic1" name="implies"/> <OMA> <OMS cd="relation1" name="neq"/> <OMV name="a"/> <OMS cd="alg1" name="zero"/> </OMA> <OMA> <OMS cd="relation1" name="eq"/> <OMA> <OMS cd="arith1" name="divide"/> <OMV name="a"/> <OMV name="a"/> </OMA> <OMS cd="alg1" name="one"/> </OMA> </OMA> </OMBIND> </OMOBJ> </FMP> </CDDefinition> <CDDefinition> <Name> power </Name> <Role>application</Role> <Description> This symbol represents a power function. The first argument is raised to the power of the second argument. When the second argument is not an integer, powering is defined in terms of exponentials and logarithms for the complex and real numbers. This operator can represent general powering. </Description> <CMP> x\in C implies x^a = exp(a ln x) </CMP> <FMP> <OMOBJ xmlns="http://www.openmath.org/OpenMath" version="2.0" cdbase="http://www.openmath.org/cd"> <OMA> <OMS cd="logic1" name="implies"/> <OMA> <OMS cd="set1" name="in"/> <OMV name="x"/> <OMS cd="setname1" name="C"/> </OMA> <OMA> <OMS cd="relation1" name="eq"/> <OMA> <OMS name="power" cd="arith1"/> <OMV name="x"/> <OMV name="a"/> </OMA> <OMA> <OMS name="exp" cd="transc1"/> <OMA> <OMS name="times" cd="arith1"/> <OMV name="a"/> <OMA> <OMS name="ln" cd="transc1"/> <OMV name="x"/> </OMA> </OMA> </OMA> </OMA> </OMA> </OMOBJ> </FMP> <CMP> if n is an integer then x^0 = 1, x^n = x * x^(n-1) </CMP> <FMP> <OMOBJ xmlns="http://www.openmath.org/OpenMath" version="2.0" cdbase="http://www.openmath.org/cd"> <OMA> <OMS cd="logic1" name="implies"/> <OMA> <OMS cd="set1" name="in"/> <OMV name="n"/> <OMS cd="setname1" name="Z"/> </OMA> <OMA> <OMS cd="logic1" name="and"/> <OMA> <OMS cd="relation1" name="eq"/> <OMA> <OMS cd="arith1" name="power"/> <OMV name="x"/> <OMI>0</OMI> </OMA> <OMS cd="alg1" name="one"/> </OMA> <OMA> <OMS cd="relation1" name="eq"/> <OMA> <OMS cd="arith1" name="power"/> <OMV name="x"/> <OMV name="n"/> </OMA> <OMA> <OMS cd="arith1" name="times"/> <OMV name="x"/> <OMA> <OMS cd="arith1" name="power"/> <OMV name="x"/> <OMA> <OMS cd="arith1" name="minus"/> <OMV name="n"/> <OMI>1</OMI> </OMA> </OMA> </OMA> </OMA> </OMA> </OMA> </OMOBJ> </FMP> <Example> <OMOBJ xmlns="http://www.openmath.org/OpenMath" version="2.0" cdbase="http://www.openmath.org/cd"> <OMA> <OMS cd="relation1" name="eq"/> <OMA> <OMS cd="arith1" name="power"/> <OMA> <OMS cd="linalg2" name="matrix"/> <OMA> <OMS cd="linalg2" name="matrixrow"/> <OMI> 1 </OMI> <OMI> 2 </OMI> </OMA> <OMA> <OMS cd="linalg2" name="matrixrow"/> <OMI> 3 </OMI> <OMI> 4 </OMI> </OMA> </OMA> <OMI>3</OMI> </OMA> <OMA> <OMS cd="linalg2" name="matrix"/> <OMA> <OMS cd="linalg2" name="matrixrow"/> <OMI> 37 </OMI> <OMI> 54 </OMI> </OMA> <OMA> <OMS cd="linalg2" name="matrixrow"/> <OMI> 81 </OMI> <OMI> 118 </OMI> </OMA> </OMA> </OMA> </OMOBJ> </Example> <Example> <OMOBJ xmlns="http://www.openmath.org/OpenMath" version="2.0" cdbase="http://www.openmath.org/cd"> <OMA> <OMS cd="relation1" name="eq"/> <OMA> <OMS cd="arith1" name="power"/> <OMS cd="nums1" name="e"/> <OMA> <OMS cd="arith1" name="times"/> <OMS cd="nums1" name="i"/> <OMS cd="nums1" name="pi"/> </OMA> </OMA> <OMA> <OMS cd="arith1" name="unary_minus"/> <OMS cd="alg1" name="one"/> </OMA> </OMA> </OMOBJ> </Example> </CDDefinition> <CDDefinition> <Name> abs </Name> <Role>application</Role> <Description> A unary operator which represents the absolute value of its argument. The argument should be numerically valued. In the complex case this is often referred to as the modulus. </Description> <CMP> for all x,y | abs(x) + abs(y) >= abs(x+y) </CMP> <FMP> <OMOBJ xmlns="http://www.openmath.org/OpenMath" version="2.0" cdbase="http://www.openmath.org/cd"> <OMBIND> <OMS cd="quant1" name="forall"/> <OMBVAR> <OMV name="x"/> <OMV name="y"/> </OMBVAR> <OMA> <OMS cd="relation1" name="geq"/> <OMA> <OMS cd="arith1" name="plus"/> <OMA> <OMS cd="arith1" name="abs"/> <OMV name="x"/> </OMA> <OMA> <OMS cd="arith1" name="abs"/> <OMV name="y"/> </OMA> </OMA> <OMA> <OMS cd="arith1" name="abs"/> <OMA> <OMS cd="arith1" name="plus"/> <OMV name="x"/> <OMV name="y"/> </OMA> </OMA> </OMA> </OMBIND> </OMOBJ> </FMP> </CDDefinition> <CDDefinition> <Name> root </Name> <Role>application</Role> <Description> A binary operator which represents its first argument "lowered" to its n'th root where n is the second argument. This is the inverse of the operation represented by the power symbol defined in this CD. Care should be taken as to the precise meaning of this operator, in particular which root is represented, however it is here to represent the general notion of taking n'th roots. As inferred by the signature relevant to this symbol, the function represented by this symbol is the single valued function, the specific root returned is the one indicated by the first CMP. Note also that the converse of the second CMP is not valid in general. </Description> <CMP> x\in C implies root(x,n) = exp(ln(x)/n) </CMP> <FMP> <OMOBJ xmlns="http://www.openmath.org/OpenMath" version="2.0" cdbase="http://www.openmath.org/cd"> <OMA> <OMS cd="logic1" name="implies"/> <OMA> <OMS cd="set1" name="in"/> <OMV name="x"/> <OMS cd="setname1" name="C"/> </OMA> <OMA> <OMS cd="relation1" name="eq"/> <OMA> <OMS cd="arith1" name="root"/> <OMV name="x"/> <OMV name="n"/> </OMA> <OMA> <OMS name="exp" cd="transc1"/> <OMA> <OMS name="divide" cd="arith1"/> <OMA> <OMS name="ln" cd="transc1"/> <OMV name="x"/> </OMA> <OMV name="n"/> </OMA> </OMA> </OMA> </OMA> </OMOBJ> </FMP> <CMP> for all a,n | power(root(a,n),n) = a (if the root exists!) </CMP> <FMP> <OMOBJ xmlns="http://www.openmath.org/OpenMath" version="2.0" cdbase="http://www.openmath.org/cd"> <OMBIND> <OMS cd="quant1" name="forall"/> <OMBVAR> <OMV name="a"/> <OMV name="n"/> </OMBVAR> <OMA> <OMS cd="relation1" name="eq"/> <OMA> <OMS cd="arith1" name="power"/> <OMA> <OMS cd="arith1" name="root"/> <OMV name="a"/> <OMV name="n"/> </OMA> <OMV name="n"/> </OMA> <OMV name="a"/> </OMA> </OMBIND> </OMOBJ> </FMP> </CDDefinition> <CDDefinition> <Name> sum </Name> <Role>application</Role> <Description> An operator taking two arguments, the first being the range of summation, e.g. an integral interval, the second being the function to be summed. Note that the sum may be over an infinite interval. </Description> <Example> This represents the summation of the reciprocals of all the integers between 1 and 10 inclusive. <OMOBJ xmlns="http://www.openmath.org/OpenMath" version="2.0" cdbase="http://www.openmath.org/cd"> <OMA> <OMS cd="arith1" name="sum"/> <OMA> <OMS cd="interval1" name="integer_interval"/> <OMI> 1 </OMI> <OMI> 10 </OMI> </OMA> <OMBIND> <OMS cd="fns1" name="lambda"/> <OMBVAR> <OMV name="x"/> </OMBVAR> <OMA> <OMS cd="arith1" name="divide"/> <OMI> 1 </OMI> <OMV name="x"/> </OMA> </OMBIND> </OMA> </OMOBJ> </Example> </CDDefinition> <CDDefinition> <Name> product </Name> <Role>application</Role> <Description> An operator taking two arguments, the first being the range of multiplication e.g. an integral interval, the second being the function to be multiplied. Note that the product may be over an infinite interval. </Description> <Example> This represents the statement that the factorial of n is equal to the product of all the integers between 1 and n inclusive. <OMOBJ xmlns="http://www.openmath.org/OpenMath" version="2.0" cdbase="http://www.openmath.org/cd"> <OMA> <OMS cd="relation1" name="eq"/> <OMA> <OMS cd="integer1" name="factorial"/> <OMV name="n"/> </OMA> <OMA> <OMS cd="arith1" name="product"/> <OMA> <OMS cd="interval1" name="integer_interval"/> <OMI> 1 </OMI> <OMV name="n"/> </OMA> <OMBIND> <OMS cd="fns1" name="lambda"/> <OMBVAR> <OMV name="i"/> </OMBVAR> <OMV name="i"/> </OMBIND> </OMA> </OMA> </OMOBJ> </Example> </CDDefinition> </CD>
<CDSignatures xmlns="http://www.openmath.org/OpenMathCDS" type="sts" cd="arith1"> <CDSStatus> official </CDSStatus> <CDSComment> Date: 1999-11-26 Author: David Carlisle </CDSComment> <Signature name="lcm"> <OMOBJ xmlns="http://www.openmath.org/OpenMath"> <OMA> <OMS name="mapsto" cd="sts"/> <OMA> <OMS name="nassoc" cd="sts"/> <OMV name="SemiGroup"/> </OMA> <OMV name="SemiGroup"/> </OMA> </OMOBJ> </Signature> <Signature name="gcd"> <OMOBJ xmlns="http://www.openmath.org/OpenMath"> <OMA> <OMS name="mapsto" cd="sts"/> <OMA> <OMS name="nassoc" cd="sts"/> <OMV name="SemiGroup"/> </OMA> <OMV name="SemiGroup"/> </OMA> </OMOBJ> </Signature> <Signature name="plus"> <OMOBJ xmlns="http://www.openmath.org/OpenMath"> <OMA> <OMS name="mapsto" cd="sts"/> <OMA> <OMS name="nassoc" cd="sts"/> <OMV name="AbelianSemiGroup"/> </OMA> <OMV name="AbelianSemiGroup"/> </OMA> </OMOBJ> </Signature> <Signature name="unary_minus"> <OMOBJ xmlns="http://www.openmath.org/OpenMath"> <OMA> <OMS name="mapsto" cd="sts"/> <OMV name="AbelianGroup"/> <OMV name="AbelianGroup"/> </OMA> </OMOBJ> </Signature> <Signature name="minus"> <OMOBJ xmlns="http://www.openmath.org/OpenMath"> <OMA> <OMS name="mapsto" cd="sts"/> <OMV name="AbelianGroup"/> <OMV name="AbelianGroup"/> <OMV name="AbelianGroup"/> </OMA> </OMOBJ> </Signature> <Signature name="times"> <OMOBJ xmlns="http://www.openmath.org/OpenMath"> <OMA> <OMS name="mapsto" cd="sts"/> <OMA> <OMS name="nassoc" cd="sts"/> <OMV name="SemiGroup"/> </OMA> <OMV name="SemiGroup"/> </OMA> </OMOBJ> </Signature> <Signature name="divide"> <OMOBJ xmlns="http://www.openmath.org/OpenMath"> <OMA> <OMS name="mapsto" cd="sts"/> <OMV name="AbelianGroup"/> <OMV name="AbelianGroup"/> <OMV name="AbelianGroup"/> </OMA> </OMOBJ> </Signature> <Signature name="power"> <OMOBJ xmlns="http://www.openmath.org/OpenMath"> <OMA> <OMS name="mapsto" cd="sts"/> <OMS name="NumericalValue" cd="sts"/> <OMS name="NumericalValue" cd="sts"/> <OMS name="NumericalValue" cd="sts"/> </OMA> </OMOBJ> </Signature> <Signature name="abs"> <OMOBJ xmlns="http://www.openmath.org/OpenMath"> <OMA> <OMS name="mapsto" cd="sts"/> <OMS name="C" cd="setname1"/> <OMS name="R" cd="setname1"/> </OMA> </OMOBJ> </Signature> <Signature name="root"> <OMOBJ xmlns="http://www.openmath.org/OpenMath"> <OMA> <OMS name="mapsto" cd="sts"/> <OMS name="NumericalValue" cd="sts"/> <OMS name="NumericalValue" cd="sts"/> <OMS name="NumericalValue" cd="sts"/> </OMA> </OMOBJ> </Signature> <Signature name="sum"> <OMOBJ xmlns="http://www.openmath.org/OpenMath"> <OMA> <OMS name="mapsto" cd="sts"/> <OMV name="IntegerRange"/> <OMA> <OMS name="mapsto" cd="sts"/> <OMS name="Z" cd="setname1"/> <OMV name="AbelianMonoid"/> </OMA> <OMV name="AbelianMonoid"/> </OMA> </OMOBJ> </Signature> <Signature name="product"> <OMOBJ xmlns="http://www.openmath.org/OpenMath"> <OMA> <OMS name="mapsto" cd="sts"/> <OMV name="IntegerRange"/> <OMA> <OMS name="mapsto" cd="sts"/> <OMS name="Z" cd="setname1"/> <OMV name="AbelianMonoid"/> </OMA> <OMV name="AbelianMonoid"/> </OMA> </OMOBJ> </Signature> </CDSignatures>
<CDGroup xmlns="http://www.openmath.org/OpenMathCDG"> <CDGroupName>mathml</CDGroupName> <CDGroupVersion> 2 </CDGroupVersion> <CDGroupRevision> 0 </CDGroupRevision> <CDGroupURL>http://www.openmath.org/cdfiles/cdgroups/mathml.cdg</CDGroupURL> <CDGroupDescription> MathML compatibility CD Group </CDGroupDescription> <CDComment>Algebra</CDComment> <CDGroupMember> <CDName>alg1</CDName> <CDURL>http://www.openmath.org/cd/alg1.ocd</CDURL> </CDGroupMember> <CDComment>Arithmetic</CDComment> <CDGroupMember> <CDName>arith1</CDName> <CDURL>http://www.openmath.org/cd/arith1.ocd</CDURL> </CDGroupMember> <CDComment>Constructor for Floating Point Numbers</CDComment> <CDGroupMember> <CDName>bigfloat1</CDName> <CDURL>http://www.openmath.org/cd/bigfloat1.ocd</CDURL> </CDGroupMember> <CDComment>Calculus</CDComment> <CDGroupMember> <CDName>calculus1</CDName> <CDURL>http://www.openmath.org/cd/calculus1.ocd</CDURL> </CDGroupMember> <CDComment>Operations on and constructors for complex numbers</CDComment> <CDGroupMember> <CDName>complex1</CDName> <CDURL>http://www.openmath.org/cd/complex1.ocd</CDURL> </CDGroupMember> <CDComment>Functions on functions</CDComment> <CDGroupMember> <CDName>fns1</CDName> <CDURL>http://www.openmath.org/cd/fns1.ocd</CDURL> </CDGroupMember> <CDComment>Integer arithmetic</CDComment> <CDGroupMember> <CDName>integer1</CDName> <CDURL>http://www.openmath.org/cd/integer1.ocd</CDURL> </CDGroupMember> <CDComment>Intervals</CDComment> <CDGroupMember> <CDName>interval1</CDName> <CDURL>http://www.openmath.org/cd/interval1.ocd</CDURL> </CDGroupMember> <CDComment>Linear Algebra - vector & matrix constructors, those symbols which are independant of orientation, but in MathML</CDComment> <CDGroupMember> <CDName>linalg1</CDName> <CDURL>http://www.openmath.org/cd/linalg1.ocd</CDURL> </CDGroupMember> <CDComment>Linear Algebra - vector & matrix constructors, those symbols which are dependant of orientation, and in MathML</CDComment> <CDGroupMember> <CDName>linalg2</CDName> <CDURL>http://www.openmath.org/cd/linalg2.ocd</CDURL> </CDGroupMember> <CDComment>Limits of unary functions</CDComment> <CDGroupMember> <CDName>limit1</CDName> <CDURL>http://www.openmath.org/cd/limit1.ocd</CDURL> </CDGroupMember> <CDComment>List constructors</CDComment> <CDGroupMember> <CDName>list1</CDName> <CDURL>http://www.openmath.org/cd/list1.ocd</CDURL> </CDGroupMember> <CDComment>Basic logical operators</CDComment> <CDGroupMember> <CDName>logic1</CDName> <CDURL>http://www.openmath.org/cd/logic1.ocd</CDURL> </CDGroupMember> <CDComment> MathML Numerical Types </CDComment> <CDGroupMember> <CDName>mathmltypes</CDName> <CDURL>http://www.openmath.org/cd/mathmltypes.ocd</CDURL> </CDGroupMember> <CDComment> MathML attributes </CDComment> <CDGroupMember> <CDName>mathmlattr</CDName> <CDURL>http://www.openmath.org/cd/mathmlattr.ocd</CDURL> </CDGroupMember> <CDComment> MathML Keys </CDComment> <CDGroupMember> <CDName>mathmlkeys</CDName> <CDURL>http://www.openmath.org/cd/mathmlkeys.ocd</CDURL> </CDGroupMember> <CDComment>Minima and maxima</CDComment> <CDGroupMember> <CDName>minmax1</CDName> <CDURL>http://www.openmath.org/cd/minmax1.ocd</CDURL> </CDGroupMember> <CDComment>Multset-theoretic operators and constructors</CDComment> <CDGroupMember> <CDName>multiset1</CDName> <CDURL>http://www.openmath.org/cd/multiset1.ocd</CDURL> </CDGroupMember> <CDComment>Symbols for creating numbers, including some defined constants (which can be seen as nullary constructors)</CDComment> <CDGroupMember> <CDName>nums1</CDName> <CDURL>http://www.openmath.org/cd/nums1.ocd</CDURL> </CDGroupMember> <CDComment>Symbols for creating piecewise definitions</CDComment> <CDGroupMember> <CDName>piece1</CDName> <CDURL>http://www.openmath.org/cd/piece1.ocd</CDURL> </CDGroupMember> <CDComment>The basic quantifiers forall and exists.</CDComment> <CDGroupMember> <CDName>quant1</CDName> <CDURL>http://www.openmath.org/cd/quant1.ocd</CDURL> </CDGroupMember> <CDComment>Common arithmetic relations</CDComment> <CDGroupMember> <CDName>relation1</CDName> <CDURL>http://www.openmath.org/cd/relation1.ocd</CDURL> </CDGroupMember> <CDComment>Number sets</CDComment> <CDGroupMember> <CDName>setname1</CDName> <CDURL>http://www.openmath.org/cd/setname1.ocd</CDURL> </CDGroupMember> <CDComment>Rounding</CDComment> <CDGroupMember> <CDName>rounding1</CDName> <CDURL>http://www.openmath.org/cd/rounding1.ocd</CDURL> </CDGroupMember> <CDComment>Set-theoretic operators and constructors</CDComment> <CDGroupMember> <CDName>set1</CDName> <CDURL>http://www.openmath.org/cd/set1.ocd</CDURL> </CDGroupMember> <CDComment>Basic data orientated statistical operators</CDComment> <CDGroupMember> <CDName>s_data1</CDName> <CDURL>http://www.openmath.org/cd/s_data1.ocd</CDURL> </CDGroupMember> <CDComment>Basic random variable orientated statistical operators</CDComment> <CDGroupMember> <CDName>s_dist1</CDName> <CDURL>http://www.openmath.org/cd/s_dist1.ocd</CDURL> </CDGroupMember> <CDComment>Basic transcendental functions</CDComment> <CDGroupMember> <CDName>transc1</CDName> <CDURL>http://www.openmath.org/cd/transc1.ocd</CDURL> </CDGroupMember> <CDComment>Vector calculus functions</CDComment> <CDGroupMember> <CDName>veccalc1</CDName> <CDURL>http://www.openmath.org/cd/veccalc1.ocd</CDURL> </CDGroupMember> <CDComment>Alternative encoding symbols for compatibility with the MathML Semantic mapping constructs.</CDComment> <CDGroupMember> <CDName>altenc</CDName> <CDURL>http://www.openmath.org/cd/altenc.ocd</CDURL> </CDGroupMember> </CDGroup>
<CD xmlns="http://www.openmath.org/OpenMathCD"> <CDComment> This document is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. The copyright holder grants you permission to redistribute this document freely as a verbatim copy. Furthermore, the copyright holder permits you to develop any derived work from this document provided that the following conditions are met. a) The derived work acknowledges the fact that it is derived from this document, and maintains a prominent reference in the work to the original source. b) The fact that the derived work is not the original OpenMath document is stated prominently in the derived work. Moreover if both this document and the derived work are Content Dictionaries then the derived work must include a different CDName element, chosen so that it cannot be confused with any works adopted by the OpenMath Society. In particular, if there is a Content Dictionary Group whose name is, for example, `math' containing Content Dictionaries named `math1', `math2' etc., then you should not name a derived Content Dictionary `mathN' where N is an integer. However you are free to name it `private_mathN' or some such. This is because the names `mathN' may be used by the OpenMath Society for future extensions. c) The derived work is distributed under terms that allow the compilation of derived works, but keep paragraphs a) and b) intact. The simplest way to do this is to distribute the derived work under the OpenMath license, but this is not a requirement. If you have questions about this license please contact the OpenMath society at http://www.openmath.org. </CDComment> <CDName> error </CDName> <CDBase>http://www.openmath.org/cd</CDBase> <CDURL> http://www.openmath.org/cd/error.ocd </CDURL> <CDReviewDate>2006-03-30</CDReviewDate> <CDStatus> official </CDStatus> <CDDate>2004-03-30</CDDate> <CDVersion>3</CDVersion> <CDRevision>0</CDRevision> <CDDefinition> <Name> unhandled_symbol </Name> <Role>error</Role> <Description> This symbol represents the error which is raised when an application reads a symbol which is present in the mentioned content dictionary, but which it has not implemented. When receiving such a symbol, the application should act as if it had received the OpenMath error object constructed from unhandled_symbol and the unhandled symbol as in the example below. </Description> <Example> The application does not implement the Complex numbers: <OMOBJ xmlns="http://www.openmath.org/OpenMath" version="2.0" cdbase="http://www.openmath.org/cd"> <OME> <OMS cd="error" name="unhandled_symbol"/> <OMS cd="setname1" name="C"/> </OME> </OMOBJ> </Example> </CDDefinition> <CDDefinition> <Name> unexpected_symbol </Name> <Role>error</Role> <Description> This symbol represents the error which is raised when an application reads a symbol which is not present in the mentioned content dictionary. When receiving such a symbol, the application should act as if it had received the OpenMath error object constructed from unexpected_symbol and the unexpected symbol as in the example below. </Description> <Example> The application received a mistyped symbol <OMOBJ xmlns="http://www.openmath.org/OpenMath" version="2.0" cdbase="http://www.openmath.org/cd"> <OME> <OMS cd="error" name="unexpected_symbol"/> <OMS cd="arith1" name="plurse"/> </OME> </OMOBJ> </Example> </CDDefinition> <CDDefinition> <Name> unsupported_CD </Name> <Role>error</Role> <Description> This symbol represents the error which is raised when an application reads a symbol where the mentioned content dictionary is not present. When receiving such a symbol, the application should act as if it had received the OpenMath error object constructed from unsupported_CD and the symbol from the unsupported Content Dictionary as in the example below. </Description> <Example> The application does not know about the CD specfun1 <OMOBJ xmlns="http://www.openmath.org/OpenMath" version="2.0" cdbase="http://www.openmath.org/cd"> <OME> <OMS cd="error" name="unsupported_CD"/> <OMS cd="specfun1" name="BesselJ"/> </OME> </OMOBJ> </Example> </CDDefinition> </CD>
This is the Relax NG Schema described in Section 3.1 expressed according to the Relax NG XML Syntax.
<grammar xmlns="http://relaxng.org/ns/structure/1.0" ns="http://www.openmath.org/OpenMath" datatypeLibrary="http://www.w3.org/2001/XMLSchema-datatypes"> <start> <ref name="OMOBJ"/> </start> <!-- OpenMath object constructor --> <define name="OMOBJ"> <element name="OMOBJ"> <ref name="compound.attributes"/> <optional> <attribute name="version"> <data type="string"/> </attribute> </optional> <ref name="omel"/> </element> </define> <!-- Elements which can appear inside an OpenMath object --> <define name="omel"> <choice> <ref name="OMS"/> <ref name="OMV"/> <ref name="OMI"/> <ref name="OMB"/> <ref name="OMSTR"/> <ref name="OMF"/> <ref name="OMA"/> <ref name="OMBIND"/> <ref name="OME"/> <ref name="OMATTR"/> <ref name="OMR"/> </choice> </define> <!-- things which can be variables --> <define name="omvar"> <choice> <ref name="OMV"/> <ref name="attvar"/> </choice> </define> <define name="attvar"> <element name="OMATTR"> <ref name="common.attributes"/> <group> <ref name="OMATP"/> <choice> <ref name="OMV"/> <ref name="attvar"/> </choice> </group> </element> </define> <define name="cdbase"> <optional> <attribute name="cdbase"> <data type="anyURI"/> </attribute> </optional> </define> <!-- attributes common to all elements --> <define name="common.attributes"> <optional> <attribute name="id"> <data type="ID"/> </attribute> </optional> </define> <!-- attributes common to all elements that construct compount OM objects. --> <define name="compound.attributes"> <ref name="common.attributes"/> <ref name="cdbase"/> </define> <!-- symbol --> <define name="OMS"> <element name="OMS"> <ref name="common.attributes"/> <attribute name="name"> <data type="NCName"/> </attribute> <attribute name="cd"> <data type="NCName"/> </attribute> <ref name="cdbase"/> </element> </define> <!-- variable --> <define name="OMV"> <element name="OMV"> <ref name="common.attributes"/> <attribute name="name"> <data type="NCName"/> </attribute> </element> </define> <!-- integer --> <define name="OMI"> <element name="OMI"> <ref name="common.attributes"/> <data type="string"> <param name="pattern">\s*(-\s?)?[0-9]+(\s[0-9]+)*\s*</param> </data> </element> </define> <!-- byte array --> <define name="OMB"> <element name="OMB"> <ref name="common.attributes"/> <data type="base64Binary"/> </element> </define> <!-- string --> <define name="OMSTR"> <element name="OMSTR"> <ref name="common.attributes"/> <text/> </element> </define> <!-- IEEE floating point number --> <define name="OMF"> <element name="OMF"> <ref name="common.attributes"/> <choice> <attribute name="dec"> <data type="double"/> </attribute> <attribute name="hex"> <data type="string"> <param name="pattern">[0-9A-F]+</param> </data> </attribute> </choice> </element> </define> <!-- apply constructor --> <define name="OMA"> <element name="OMA"> <ref name="compound.attributes"/> <oneOrMore> <ref name="omel"/> </oneOrMore> </element> </define> <!-- binding constructor --> <define name="OMBIND"> <element name="OMBIND"> <ref name="compound.attributes"/> <ref name="omel"/> <ref name="OMBVAR"/> <ref name="omel"/> </element> </define> <!-- variables used in binding constructor --> <define name="OMBVAR"> <element name="OMBVAR"> <ref name="common.attributes"/> <oneOrMore> <ref name="omvar"/> </oneOrMore> </element> </define> <!-- error constructor --> <define name="OME"> <element name="OME"> <ref name="common.attributes"/> <ref name="OMS"/> <zeroOrMore> <choice> <ref name="omel"/> <ref name="OMFOREIGN"/> </choice> </zeroOrMore> </element> </define> <!-- attribution constructor and attribute pair constructor --> <define name="OMATTR"> <element name="OMATTR"> <ref name="compound.attributes"/> <ref name="OMATP"/> <ref name="omel"/> </element> </define> <define name="OMATP"> <element name="OMATP"> <ref name="compound.attributes"/> <oneOrMore> <ref name="OMS"/> <choice> <ref name="omel"/> <ref name="OMFOREIGN"/> </choice> </oneOrMore> </element> </define> <!-- foreign constructor --> <define name="OMFOREIGN"> <element name="OMFOREIGN"> <ref name="compound.attributes"/> <optional> <attribute name="encoding"> <data type="string"/> </attribute> </optional> <zeroOrMore> <choice> <ref name="omel"/> <ref name="notom"/> </choice> </zeroOrMore> </element> </define> <!-- Any elements not in the om namespace (valid om is allowed as a descendant) --> <define name="notom"> <choice> <element> <anyName> <except> <nsName/> </except> </anyName> <zeroOrMore> <attribute> <anyName/> </attribute> </zeroOrMore> <zeroOrMore> <choice> <ref name="omel"/> <ref name="notom"/> </choice> </zeroOrMore> </element> <text/> </choice> </define> <!-- reference constructor --> <define name="OMR"> <element name="OMR"> <ref name="common.attributes"/> <attribute name="href"> <data type="anyURI"/> </attribute> </element> </define> </grammar>
Relax NG allows one to state constraints such as
if the cd attribute of OMS is arith1 then the name attribute must be
one of lcm, gcd, plus etc. Thus it is easy to use a
stylesheet to generate for any given CD, a Relax NG schema that
expresses the constraint that an OMS naming
that CD must only use symbols defined in the specified dictionary.
Similarly it is possible to use the role
information contained in the CD to restrict which symbols can be the
first child of an OMBIND or the odd-numbered
children of an OMATP.
The modularisation mechanisms of Relax NG then allow one to
include these schema for all the CDs that you want to allow and, for
example, to replace the regexp-based validation of the
OMS attributes by explicit lists of allowed
CD names, and for each CD Name, a list of allowed symbol names.
For example, a CD-specific Relax NG Schema for the arith1 CD shown in Appendix A.2 would look like:
<?xml version="1.0" encoding="UTF-8"?>
<grammar xmlns="http://relaxng.org/ns/structure/1.0" datatypeLibrary="">
<define name="cd.attlist.OMS" combine="choice">
<attribute name="cd">
<value type="string">arith1</value>
</attribute>
<attribute name="name">
<choice>
<value type="string">lcm</value>
<value type="string">gcd</value>
<value type="string">plus</value>
<value type="string">unary_minus</value>
<value type="string">minus</value>
<value type="string">times</value>
<value type="string">divide</value>
<value type="string">power</value>
<value type="string">abs</value>
<value type="string">root</value>
<value type="string">sum</value>
<value type="string">product</value>
</choice>
</attribute>
</define>
</grammar>
or, using the Relax NG compact syntax:
cd.attlist.OMS |=
attribute cd {string "arith1" },
attribute name {
string "lcm" |
string "gcd" |
string "plus" |
string "unary_minus" |
string "minus" |
string "times" |
string "divide" |
string "power" |
string "abs" |
string "root" |
string "sum" |
string "product" }
To build a schema that allows only symbols from arith1 we just need to include the OpenMath schema described in Section 3.1.1, override the attribute declarations for OMS, and then include the schema for arith1. For example:
<?xml version="1.0" encoding="UTF-8"?>
<grammar xmlns="http://relaxng.org/ns/structure/1.0">
<include href="openmath.rng">
<define name="attlist.OMS">
<ref name="cd.attlist.OMS"/>
</define>
</include>
<include href="arith1.rng"/>
</grammar>
or, in the compact syntax:
include "openmath.rnc" {
attlist.OMS = cd.attlist.OMS}
include "arith1.rnc"
Using this approach it is possible to include as many files as required.
This is an XSD Schema generated from the Relax NG Schema described in Section 3.1.
<schema xmlns:xs="http://www.w3.org/2001/XMLSchema" xmlns:om="http://www.openmath.org/OpenMath" elementFormDefault="qualified" targetNamespace="http://www.openmath.org/OpenMath"> <!-- OpenMath object constructor --> <element name="OMOBJ"> <complexType> <group ref="om:omel"/> <attributeGroup ref="om:compound.attributes"/> <attribute name="version" type="xs:string"/> </complexType> </element> <!-- Elements which can appear inside an OpenMath object --> <group name="omel"> <choice> <element ref="om:OMS"/> <element ref="om:OMV"/> <element ref="om:OMI"/> <element ref="om:OMB"/> <element ref="om:OMSTR"/> <element ref="om:OMF"/> <element ref="om:OMA"/> <element ref="om:OMBIND"/> <element ref="om:OME"/> <group ref="om:OMATTR"/> <element ref="om:OMR"/> </choice> </group> <!-- things which can be variables --> <group name="omvar"> <choice> <element ref="om:OMV"/> <group ref="om:attvar"/> </choice> </group> <group name="attvar"> <sequence> <element name="OMATTR"> <complexType> <sequence> <element ref="om:OMATP"/> <choice> <element ref="om:OMV"/> <group ref="om:attvar"/> </choice> </sequence> <attributeGroup ref="om:common.attributes"/> </complexType> </element> </sequence> </group> <attributeGroup name="cdbase"> <attribute name="cdbase" type="xs:anyURI"/> </attributeGroup> <!-- attributes common to all elements --> <attributeGroup name="common.attributes"> <attribute name="id" type="xs:ID"/> </attributeGroup> <!-- attributes common to all elements that construct compount OM objects. --> <attributeGroup name="compound.attributes"> <attributeGroup ref="om:common.attributes"/> <attributeGroup ref="om:cdbase"/> </attributeGroup> <!-- symbol --> <element name="OMS"> <complexType> <attributeGroup ref="om:common.attributes"/> <attribute name="name" use="required" type="xs:NCName"/> <attribute name="cd" use="required" type="xs:NCName"/> <attributeGroup ref="om:cdbase"/> </complexType> </element> <!-- variable --> <element name="OMV"> <complexType> <attributeGroup ref="om:common.attributes"/> <attribute name="name" use="required" type="xs:NCName"/> </complexType> </element> <!-- integer --> <element name="OMI"> <complexType> <simpleContent> <restriction base="xs:anyType"> <simpleType> <restriction base="xs:string"> <pattern value="\s*(-\s?)?[0-9]+(\s[0-9]+)*\s*"/> </restriction> </simpleType> <attributeGroup ref="om:common.attributes"/> </restriction> </simpleContent> </complexType> </element> <!-- byte array --> <element name="OMB"> <complexType> <simpleContent> <extension base="xs:base64Binary"> <attributeGroup ref="om:common.attributes"/> </extension> </simpleContent> </complexType> </element> <!-- string --> <element name="OMSTR"> <complexType mixed="true"> <attributeGroup ref="om:common.attributes"/> </complexType> </element> <!-- IEEE floating point number --> <element name="OMF"> <complexType> <attributeGroup ref="om:common.attributes"/> <attribute name="dec" type="xs:double"/> <attribute name="hex"> <simpleType> <restriction base="xs:string"> <pattern value="[0-9A-F]+"/> </restriction> </simpleType> </attribute> </complexType> </element> <!-- apply constructor --> <element name="OMA"> <complexType> <group maxOccurs="unbounded" ref="om:omel"/> <attributeGroup ref="om:compound.attributes"/> </complexType> </element> <!-- binding constructor --> <element name="OMBIND"> <complexType> <sequence> <group ref="om:omel"/> <element ref="om:OMBVAR"/> <group ref="om:omel"/> </sequence> <attributeGroup ref="om:compound.attributes"/> </complexType> </element> <!-- variables used in binding constructor --> <element name="OMBVAR"> <complexType> <group maxOccurs="unbounded" ref="om:omvar"/> <attributeGroup ref="om:common.attributes"/> </complexType> </element> <!-- error constructor --> <element name="OME"> <complexType> <sequence> <element ref="om:OMS"/> <choice minOccurs="0" maxOccurs="unbounded"> <group ref="om:omel"/> <element ref="om:OMFOREIGN"/> </choice> </sequence> <attributeGroup ref="om:common.attributes"/> </complexType> </element> <!-- attribution constructor and attribute pair constructor --> <group name="OMATTR"> <sequence> <element name="OMATTR"> <complexType> <sequence> <element ref="om:OMATP"/> <group ref="om:omel"/> </sequence> <attributeGroup ref="om:compound.attributes"/> </complexType> </element> </sequence> </group> <element name="OMATP"> <complexType> <sequence maxOccurs="unbounded"> <element ref="om:OMS"/> <choice> <group ref="om:omel"/> <element ref="om:OMFOREIGN"/> </choice> </sequence> <attributeGroup ref="om:compound.attributes"/> </complexType> </element> <!-- foreign constructor --> <element name="OMFOREIGN"> <complexType mixed="true"> <choice minOccurs="0" maxOccurs="unbounded"> <group ref="om:omel"/> <group ref="om:notom"/> </choice> <attributeGroup ref="om:compound.attributes"/> <attribute name="encoding" type="xs:string"/> </complexType> </element> <!-- Any elements not in the om namespace (valid om is allowed as a descendant) --> <group name="notom"> <sequence> <choice minOccurs="0"> <any namespace="##other" processContents="skip"/> <any namespace="##local" processContents="skip"/> </choice> </sequence> </group> <!-- reference constructor --> <element name="OMR"> <complexType> <attributeGroup ref="om:common.attributes"/> <attribute name="href" use="required" type="xs:anyURI"/> </complexType> </element> </schema>
This is a DTD generated from the Relax NG Schema described in
Section 3.1. Note that we cannot express the
fact that the OMFOREIGN element can
contain any well-formed XML, so we have simply restricted it to
contain any XML defined in the DTD.
<?xml encoding="UTF-8"?>
<!-- RELAX NG Schema for OpenMath 2 -->
<!ENTITY % cdbase "
cdbase CDATA #IMPLIED">
<!-- attributes common to all elements -->
<!ENTITY % common.attributes "
id ID #IMPLIED">
<!-- attributes common to all elements that construct compount OM objects. -->
<!ENTITY % compound.attributes "
%common.attributes;
%cdbase;">
<!-- Elements which can appear inside an OpenMath object -->
<!ENTITY % omel "OMS|OMV|OMI|OMB|OMSTR|OMF|OMA|OMBIND|OME|OMATTR|OMR">
<!-- OpenMath object constructor -->
<!ELEMENT OMOBJ (%omel;)>
<!ATTLIST OMOBJ
xmlns CDATA #FIXED 'http://www.openmath.org/OpenMath'
%compound.attributes;
version CDATA #IMPLIED>
<!ENTITY % attvar "OMATTR">
<!-- things which can be variables -->
<!ENTITY % omvar "OMV|%attvar;">
<!-- symbol -->
<!ELEMENT OMS EMPTY>
<!ATTLIST OMS
xmlns CDATA #FIXED 'http://www.openmath.org/OpenMath'
%common.attributes;
name NMTOKEN #REQUIRED
cd NMTOKEN #REQUIRED
%cdbase;>
<!-- variable -->
<!ELEMENT OMV EMPTY>
<!ATTLIST OMV
xmlns CDATA #FIXED 'http://www.openmath.org/OpenMath'
%common.attributes;
name NMTOKEN #REQUIRED>
<!-- integer -->
<!ELEMENT OMI (#PCDATA)>
<!ATTLIST OMI
xmlns CDATA #FIXED 'http://www.openmath.org/OpenMath'
%common.attributes;>
<!-- byte array -->
<!ELEMENT OMB (#PCDATA)>
<!ATTLIST OMB
xmlns CDATA #FIXED 'http://www.openmath.org/OpenMath'
%common.attributes;>
<!-- string -->
<!ELEMENT OMSTR (#PCDATA)>
<!ATTLIST OMSTR
xmlns CDATA #FIXED 'http://www.openmath.org/OpenMath'
%common.attributes;>
<!-- IEEE floating point number -->
<!ELEMENT OMF EMPTY>
<!ATTLIST OMF
xmlns CDATA #FIXED 'http://www.openmath.org/OpenMath'
%common.attributes;
dec CDATA #IMPLIED
hex CDATA #IMPLIED>
<!-- apply constructor -->
<!ELEMENT OMA (%omel;)+>
<!ATTLIST OMA
xmlns CDATA #FIXED 'http://www.openmath.org/OpenMath'
%compound.attributes;>
<!-- binding constructor -->
<!ELEMENT OMBIND ((%omel;),OMBVAR,(%omel;))>
<!ATTLIST OMBIND
xmlns CDATA #FIXED 'http://www.openmath.org/OpenMath'
%compound.attributes;>
<!-- variables used in binding constructor -->
<!ELEMENT OMBVAR (%omvar;)+>
<!ATTLIST OMBVAR
xmlns CDATA #FIXED 'http://www.openmath.org/OpenMath'
%common.attributes;>
<!-- error constructor -->
<!ELEMENT OME (OMS,(%omel;|OMFOREIGN)*)>
<!ATTLIST OME
xmlns CDATA #FIXED 'http://www.openmath.org/OpenMath'
%common.attributes;>
<!-- attribution constructor and attribute pair constructor -->
<!ELEMENT OMATTR (OMATP,(%omel;))>
<!ATTLIST OMATTR
xmlns CDATA #FIXED 'http://www.openmath.org/OpenMath'
%compound.attributes;>
<!ELEMENT OMATP (OMS,(%omel;|OMFOREIGN))+>
<!ATTLIST OMATP
xmlns CDATA #FIXED 'http://www.openmath.org/OpenMath'
%compound.attributes;>
<!-- foreign constructor -->
<!ELEMENT OMFOREIGN ANY>
<!ATTLIST OMFOREIGN
xmlns CDATA #FIXED 'http://www.openmath.org/OpenMath'
%compound.attributes;
encoding CDATA #IMPLIED>
<!--
Any elements not in the om namespace
(valid om is allowed as a descendant)
-->
<!-- reference constructor -->
<!ELEMENT OMR EMPTY>
<!ATTLIST OMR
xmlns CDATA #FIXED 'http://www.openmath.org/OpenMath'
%common.attributes;
href CDATA #REQUIRED>
In this appendix we describe the major changes that occurred between version 1.1 and version 2 of the OpenMath standard. All changes to the encodings and content dictionaries have been designed to be backward compatible, in other words all existing OpenMath objects and Content Dictionaries are still valid in OpenMath 2. On the other hand an existing OpenMath 1.1 application may not be able to process OpenMath 2 objects.
Additional features of abstract objects have been introduced:
OpenMath symbols have an optional role qualifier which restricts the place where they may occur within compound objects. Although part of the abstract description of a symbol this information is intended to be stored in the CD. In the XML encoding it may be used to provide a more restricted schema leading to tighter validation.
In addition to their name and cd properties, symbols now have an optional cdbase property. This can be used to disambiguate between two CDs which are produced independently but have the same name, and can also be used to produce a canonical URI for any OpenMath symbol for use in frameworks such as RDFS or MathML which need one.
An OpenMath object may be attributed with a non-OpenMath object using the new foreign constructor. This allows an XML-encoded OpenMath object to be attributed with appropriate Presentation MathML, for example, or a base-64 encoded MPEG file of its aural rendering.
In addition, an OpenMath error object may take as its arguments non-OpenMath objects wrapped in the new foreign constructor.
The new role property can be used to indicate that a symbol is an attribution, in which case an application may ignore or remove it, or a semantic attribution in which case removing it is no longer guaranteed to produce an equivalent object.
Restrictions on the names of symbols, variables and content dictionaries have been relaxed to be compatible with XML and to be less Anglo-Saxon.
The OpenMath version 2 standard still mandates two encodings: XML and binary. The XML encoding in particular has been updated to reflect the latest development of XML and is now a full XML application. Version 2 encodings are backward compatible with version 1.1 encodings.
Both encodings have been updated to support the changes to the model of abstract objects described above.
Encodings support internal and external sharing of objects
An optional attribute defining the version of the encoding can be specified for the encoded object
The XML encoding in version 2 is defined by a Relax NG schema and the mandated character-based grammar of version 1 has been removed, while the DTD has been relegated to an Appendix.
The symbolic values INF,
-INF and NaN have
been added to the decimal attribute of an OMF
in the XML encoding,
and guidelines on the interpretation of NaNs
added to the compliance section.
The Binary encoding has been extended to support the streaming of objects.
In OpenMath version 2 Content Dictionaries are defined in terms of the abstract information content that needs to be specified for defining OpenMath symbols. The current implementation is thus just one possible encoding of this abstract model.
The CDUses element is not part of this information model and has been made optional and deprecated in the reference encoding since it is trivial to extract its content automatically from the CD.
A CD may now, optionally, define its cdbase.
A CD symbol definition may now, optionally, define its role.
An FMP may, optionally, have a kind
attribute for use in classifying different kinds of definitions. The
details of how this attribute is used are not mandated by the standard.
The XML encoded Content Dictionaries now use elements from
the namespace http://www.openmath.org/OpenMathCD.
There are now explicitly two XML encodings: the previous one and the Strict Content MathML one. This necessitated changes to the preamble and the start of Chapter 3.
The description of the encoding of xfffffff1 in base 256 was corrected (the 0xab (base 256/positive) byte was omitted and 0xF1 had been written 0xFI.
The phrase "in little endian format" was unhelpfully included in the description of the binary integer encoding, which contradicted the later "network byte order". Now removed.
Section 3.1.2 described the OpenMath XML value of hex as "from lowest to highest bits using a least significant byte ordering". This wording was copied from section 4.2.1.2 of
[19], but is close to meaningless. Replaced by the current "in network byte order".
The example of binary encoding of floats in 3.2.2 "For example, 0.1 is encoded as 0x03 0x000000000000f03f" was wrong, and has been replaced by the same example as the XML encoding.
A citation to MathML 3 was added.
The "Note on names", which used to refer to Unicode 2.0, has been upgraded to allow for XML 1.0 5th edition and more specifically erratum NE17 in [16], so that the current version of Unicode is incorporated.
[1]
S. Freundt, P. Horn, A. Konovalov, S. Linton, D. Roozemond
Symbolic Computation Software Composability Protocol SCSCP Specification 1.3, March 22, 2009.
https://github.com/OpenMath/scscp/blob/master/revisions/SCSCP_1_3.pdf
[2] N. Borenstein and N. Freed MIME (Multipurpose Internet Mail Extensions) Part One: Format of Internet Message Bodies, November 1996.
http://www.ietf.org/rfc/rfc2045.txt
[3] N. Borenstein and N. Freed MIME (Multipurpose Internet Mail Extensions) Part Two: Media
Types, November 1996.
http://www.ietf.org/rfc/rfc2046.txt
[4] Olga Caprotti and Arjeh M. Cohen A Type System for OpenMath 1.3.2b OpenMath Esprit Consortium, February 1999.
http://www.openmath.org/standard/ecc.pdf
[5] J. Davenport A Small OpenMath Type System, April 1999.
http://www.openmath.org/standard/sts.pdf
[6] IEEE and The Open Group Std 1003.1, 2003 Edition, The Open Group Base Specifications Issue 6 , 2003.
http://www.unix.org/version3/ieee_std.html
[7] IETF RFC 2396 - Uniform Resource Identifiers (URI): Generic Syntax, August 1998.
http://www.ietf.org/rfc/rfc2396.txt
[8] OASIS Committee Specification RELAX NG Specification, December 2001.
http://www.oasis-open.org/committees/relax-ng/spec-20011203.html
[9] OpenMath Consortium OpenMath Version 2.0, June 2004.
http://www.openmath.org/standard/om20-2004-06-30/
[10] OpenMath Consortium OpenMath Primer, June 2004.
http://www.openmath.org/standard/primer/
[11] Technical committee / subcommittee: JTC 1 ISO 9660:1988 Information processing – Volume and File Structure of CDROM for Information Interchange, 1988.
http://www.iso.org/iso/en/CatalogueDetailPage.CatalogueDetail?CSNUMBER=17505
[12] Unicode Consortium The Unicode Standard: Version 4.0.0 Addison-Wesley, 2003.
Online edition available from http://www.unicode.org/versions/Unicode4.0.0
[13] World Wide Web Consortium XML Schema Part 1: Structures & Part 2: Datatypes, May 2001.
http://www.w3.org/TR/xmlschema-1/
http://www.w3.org/TR/xmlschema-2/
[14] World Wide Web Consortium Namespaces in XML, January 1999.
http://www.w3.org/TR/REC-xml-names/
[15] World Wide Web Consortium Extensible Markup Language (XML) 1.0., February 1998.
http://www.w3.org/TR/1998/REC-xml-19980210
[16] World Wide Web Consortium Namespaces in XML 1.0 (Second Edition) Errata, November 2008.
https://www.w3.org/XML/2006/xml-names-errata
[17] World Wide Web Consortium Extensible Markup Language (XML) 1.1. W3C Recommendation REC-xml11-20040204, February 2004.
http://www.w3.org/TR/2004/REC-xml11-20040204/
[18] World Wide Web Consortium Mathematical Markup Language (MathML) 2.0 Specification
(Second Edition), October 2003.
http://www.w3.org/TR/MathML2/
[19] World Wide Web Consortium Mathematical Markup Language (MathML) 3.0 Specification
2nd Edition, April 2014.
http://www.w3.org/TR/MathML3/
[20] World Wide Web Consortium OWL Web Ontology Language Overview , February 2004.
http://www.w3.org/TR/2004/REC-owl-features-20040210/
[21] World Wide Web Consortium Resource Description Framework (RDF): Concepts and Abstract Syntax, February 2004.
http://www.w3.org/TR/2004/REC-rdf-concepts-20040210/
[22] IEEE Standard for binary Floating-Point Arithmetic ANSI/IEEE Standard 754, 1985.
http://standards.ieee.org/reading/ieee/std_public/description/busarch/754-1985_desc.html